Mea culpa

Dans ma correction de l’avis de Recherche n° 5, je terminais ainsi :

« C’est une méthode certes artisanale mais qui me semble correcte. Qu’en pensez-vous ? »

Eh bien Salvatore Tummarello a pensé que ce n’était pas correct… et il avait bien raison.

Rappelons les faits :

Donc avec les $a$ et $b$ ainsi trouvés il me reste à prouver que l’on ne peut pas trouver d’entier $d$ vérifiant l’équation $(2)$.

Calculons $a^2+2b^2 =(-p^2+2pq+2q^2)^2+2( p^2+4pq- 2q^2)^2 = \cdots = 3(p^4 + 4p^3q + 8p^2q^2 - 8pq^3 + 4q^4) = 3 d^2$ ???

$a^2+2b^2$ étant un polynôme homogène de degré 4, $d$ doit donc être un polynôme homogène de degré 2 donc il faut trouver $k$ entier tel que $d= p^2 +kpq + 2q^2$ ($p^2$ fournissant le terme en $p^4$ et $2q^2$ fournissant le terme en $4q^4$).

En élevant cette expression de $d$ au carré nous obtenons : $p^4 + 2kp^3q + (4+k^2)p^2q^2 + 4kpq^3 + 4p^4$

Par identification nous obtenons $2k = 4, 4+k^2 =8, 4k =-8$

c’est-à-dire $k=2$ et $k = -2$ donc pas de solution.

L’erreur était grossière car comme l’écrit Salvatore :

tu as montré l’impossibilité de factoriser le polynôme $P(p,q)= p^4+ 4p^3q + 8p^2q^2 - 8pq^3 + 4q^4$ sous la forme d’un carré d’un polynôme, mais je ne vois pas en quoi cela interdit l’existence de certaines valeurs de $p$ et $q$ telles que $P(p,q)$ soit un carré. D’ailleurs $P(1,1)=3^2$

…façon polie de me faire remarquer que j’avais confondu « quelque soit » avec « il existe », même si le contre-exemple fourni est bien le seul qui existe, (avec bien sûr tous les $(n,n)$), et réduit le trapèze à n’être qu’un rectangle.

Mais le plus grave est que je n’ai toujours pas trouvé une démonstration simple de cette « évidence » et que nous devons nous contenter pour l’instant de celle de Salvatore, lourde mais correcte. Amis lecteurs, saurez-vous trouver une démonstration plus simple ?

Correction de l’Avis de Recherche n°6

Encore deux réponses seulement à cet avis de recherche et des deux mêmes auteurs… ça va finir par faire jaser !

Jean Couzineau est plutôt dans l’esprit de ces avis de recherche en exposant sa démarche, en expérimentant et en faisant vérifier les cas restants par une machine (personnellement cela ne me gêne pas mais je connais des esthètes de l’art qui ne supportent pas) et, en plus, il généralise en recherchant le plus grand entier positif répondant à la question mais avec une écriture unique !

Vous pouvez lire la solution de Jean Couzineau, en téléchargement.

Salvatore Tummarello nous bourbakise le problème en une définition, un lemme et deux propositions qui résolvent la question et pour deux propositions de plus nous donne le résultat en fonction de coefficients quelconques et non seulement $15$, $21$ et $35$.

La solution de Salvatore Tummarello à découvrir absolument, en téléchargement.

Et pourtant j’ai encore l’outrecuidance de préférer ma méthode qui fait apparaître le nombre-réponse $139$ de façon (presque) naturelle en utilisant le raisonnement par récurrence le plus basique avec une économie de calculs. Mais peut-être suis-je trop partial…

Bezout nous a appris que les nombres $15$, $21$ et $35$ étant étrangers entre eux, il existe $(a, b, c)$ tels que $15a + 21b + 35c = 1$ donc que tout nombre peut s’écrire sous cette forme mais que cela ne sera vrai qu’avec $a$, $b$ et $c$ entiers relatifs.

Par exemple,

$(1) (-6, 1, 3) : 15\times(-6) + 21\times1 + 35\times2 = 1$

$(2) (1, -4, 2) : 15\times1 + 21\times(-4) + 35\times2 = 1$

$(3) (1, 1, -1) : 15\times1 + 21\times1 + 35\times(-1) = 1$

Évidemment il existe des nombres, que nous allons appeler convenables, qui peuvent s’écrire sous la forme $15a + 21b + 35c$ avec $a$, $b$ et $c$ positifs, le plus petit étant $0$ et les suivants $15$, $21$, $35$, $36$...

Nous allons montrer, par récurrence, que la propriété d’être convenable est vraie à partir d’un certain nombre $n_0$ convenable et le nombre $n_0-1$ constituant la réponse à la question posée.

Supposons donc que $n = 15a + 21b + 35c$ soit convenable, comment écrire $n+1$ ?

• Si $a≥6$ alors $n + 1 = 15a + 21b + 35c + 15(-6) + 21 + 35 (2)$ d’après (1)

$n + 1 = 15(a - 6) + 21(b + 1) + 35(c + 2)$ qui est un nombre convenable car tous les coefficients sont positifs.

• Si $a<6$ et $b≥4$ alors (2) nous permettrait d’écrire :

$n + 1 = 15(a + 1) + 21(b - 4) + 35(c + 2)$ nombre tout aussi convenable

• Si $a<6$ et $b<4$ et $c ≥1$ alors cette fois nous utiliserons (3) pour écrire :

$n + 1 = 15(a + 1) + 21(b + 1) + 35(c - 1)$ qui encore parfaitement convenable.

• Et sinon ? Eh bien $a<6$ et $b<4$ et $c = 0$ donc $n ≤ 15\times5 +21\times3 + 35\times0 = 138$ donc convenable.

Et son successeur ? A-t-on $139 = 15a + 21b + 35c$ ?

Si cela était vrai nous aurions $4 ≡ b mod (5)$ c’est-à-dire $b=4$ seule valeur positive possible (car la suivante, $b=9$, entraîne $21 b = 189 \gt 139$).

Donc $139 – 4\times21 = 15a + 35c$ c’est-à-dire $55 = 5(3a+7c)$

D’où $11 = 3a+7c$ impossible à réaliser avec $a$ et $c$ positifs ($7=0$ et $7=1$ impossible et $7\gt1$ trop grand). Donc $139$ n’est pas convenable.

Mais $140 = 15\times7 + 21\times0 + 35\times1$ est convenable, comme tous ceux qui le suivent, ainsi que le prouve la démonstration de l’hérédité ci-dessus. Donc $n_0 = 140$ et la solution cherchée est bien $n_0 -1 = 139$.

Ce qui m’a toujours semblé bizarre dans cette démonstration, c’est que le nombre $139$ trouvé semble dépendre des 3 égalités qui paraissent choisies au hasard. Ne serait-il pas possible de trouver un autre nombre $M$ réalisant la même prouesse ?

Eh bien non.

Si $M<139$ ce ne serait pas le plus grand puisqu’il est plus petit que $139$ (!) et si $M\gt139$ alors ma démonstration prouve qu’il serait convenable (donc ne conviendrait pas !).

En réalité mes 3 égalités ne sont pas vraiment choisies au hasard : j’ai choisi pour chacune d’elle un seul nombre négatif le plus grand possible. Par exemple pour (1) : $15a + 21b + 35c = 1$ donne, modulo 7, $a ≡ 1$ et $a = - 6$ est bien le plus grand nombre négatif réalisant cela.

Idem pour les deux autres par interprétation modulo 5 pour $b$ et modulo 3 pour $c$.

Et maintenant vous savez tout !

Avis de Recherche n°7

Énoncé de l’avis de recherche n°7 :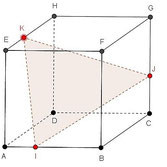 Comment placer sur ce cube $ABCDEFGH$ le point $I$ (respectivement $J$ et $K$) sur l’arête $[AB]$ (respectivement $[CG]$ et $[EH]$) pour minimaliser :   a) le périmètre du triangle $IJK$ ?   b) l’aire de ce même triangle ?   Envoyez vos réponses à esartinuloc chez gmail.com