Cet article de Servane Bertrand fait suite au Bizarre n°1 publié dans le n°158 des Chantiers de Pédagogie Mathématique.

Le problème de calcul que je vais vous présenter a été donné à mes deux classes de troisième, les identités remarquables ayant été vues et utilisées auparavant soit pour faire du calcul mental soit pour démontrer la finalité d’un programme de calcul.

Ce travail a suscité un très grand intérêt et une vive surprise des élèves et tout particulièrement d’Ibtissam purement et simplement réfractaire aux mathématiques. Ce jour là j’ai eu le plaisir de la voir s’investir pour la première fois en 2 ans dans une activité mathématique, grande victoire pour moi je ne le cache pas, mais revenons à nos moutons…

Objectif : Utilisation de nos bonnes vieilles identités remarquables pour parer aux bugs de la calculatrice ou du tableur.

Phase 1 : Calcul effectué à la calculatrice Casio fx-92 ou Texas TI-Collège

C’est le début du cours, j’écris au tableau le calcul suivant :

$$ A = 4\,513\,275\,237^2 - 4\,513\,275\,236^2$$

et demande à mes élèves de l’effectuer à la calculatrice.

Voici les résultats trouvés :

• Les utilisateurs de Casio, majoritaires, trouvent $A = 9\,000\,000\,000$
• Les utilisateurs de Texas trouvent $A = 9\,020\,000\,000$

À ce stade, les élèves sont sûrs qu’un des 2 résultats est le bon mais la différence non négligeable (20 millions tout de même) entre les 2 réponses données par leurs calculatrices les intrigue. Le verdict tombe comme un couperet sur les espoirs de mes 28 têtes brunes et blondes quand je leur annonce qu’aucune des 2 propositions n’est correcte.

Phase 2 : Repérage de l’erreur

C’est le moment de les faire chercher pour quelle raison j’en suis certaine. Mais oui, le chiffre des unités du nombre $A$ est obligatoirement 3.

Mais que donne le tableur ? Hum, le résultat n’est toujours pas le bon, il se termine par 8.

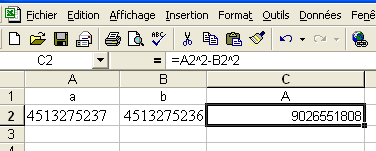
Phase 3 : Utilisation des identités remarquables

Il va falloir trouver un autre moyen pour effectuer ce calcul sans que cela soit trop fastidieux. Une observation minutieuse du calcul permet enfin d’associer $A$ à l’expression $(x + 1)^2 - x^2$ où $x$ est égal à $4\,513\,275\,236$.

Les élèves ont à leur disposition deux méthodes pour simplifier $A$, le développement ou la factorisation à l’aide des identités remarquables, et obtiennent $A = 2x + 1$.

Le calcul se fait alors sans problème : $A = 2 \times 4\,513\,275\,236 + 1 = 9\,026\,550\,473$.

Après plusieurs expérimentations, il semblerait que la calculatrice commence à dysfonctionner quand $x$ dépasse 10 millions alors que le tableur permet des valeurs de $x$ pouvant aller jusqu’à $94\,906\,264$.

Commentaire de Rémy Coste, proposition pour prolonger la phase 3

Question :

Sachant que les calculs exacts se font avec des nombres s’écrivant avec 14 chiffres au maximum, quelle est la valeur maximale de $x$ pour laquelle il n’y aura pas d’erreur ?

Réponse :

Il s’agit de calculer $(x+1)^2 - x^2$. Il faut donc (et il suffit… on l’espère…) que $(x+1)^2 \leq 10^{14}$ c’est à dire $x + 1 \leq 10^7$.

Test : en donnant à $x$ les valeurs entières à partir de $9\,999\,998$, et en comparant $(x+1)^2 - x^2$ et $2x + 1$, on constate effectivement que c’est exactement à partir de $x = 10^7$ que ça déraille.

Cela dit, on peut se demander pourquoi Casio trouve $9\,000\,000\,000$ et Texas $9\,020\,000\,000$ ? En s’aidant d’un tableur (qui donne 15 chiffres significatifs), cela permet de comprendre.

Posons $x = 4\,513\,275\,237$. D’après le tableur, on a : $(x+1)^2 = \mathbf{20\,369\,653\,3}64\,917\,4 ??\, ???$ et $x^2 = \mathbf{20\,369\,653\,3}55\,890\,9 ??\, ???$ (en gras les chiffres communs, et un ? pour chaque chiffre inconnu).

Si on arrondit ces valeurs à 12 chiffres significatifs (le 13^e chiffre sert à cela), on trouve :

$(x+1)^2 = 20\,369\,653\,364\,900\,000\,000$ et $x^2 = 20\,369\,653\,355\,900\,000\,000$.

La différence est alors égale à $=9\,000\,000\,000$, c’est ce que trouve Casio.

Si on tronque ces valeurs à 13 chiffres significatifs, on trouve :

$(x + 1)^2 = 20\,369\,653\,364\,910\,000\,000$ et $x^2 = 20\,369\,653\,355\,890\,000\,000$.

La différence est alors égale à $ 9\,020\,000\,000$, c’est ce que trouve Texas.

Conclusion :

Les calculatrices collège Casio et Texas écrivent les nombres avec 13 chiffres significatifs. Mais Casio fait les calculs avec 12 chiffres, le 13^e ne servant qu’à arrondir. Texas utilise les 13 chiffres pour les calculs.

Ce qui est curieux, c’est que la Texas lycée (TI82.STAT) écrit les nombres avec 14 chiffres, mais ne fait les calculs qu’avec 13 chiffres, le 14^e servant à arrondir… comme la Casio collège…