
par Alain Bougeard
La nouvelle mode sur internet (et en particulier sur YouTube) est le découpage des tablettes de chocolat…
Découpages subtils qui permettent de récupérer 1 (voire 2 ou 3 pour les meilleurs) carrés supplémentaires ce qui a pour résultat de faire saliver les gourmands tout en les étonnant quand même. Et l’avantage quand on est prof de math est de recevoir des liens (alors qu’on préférerait du chocolat) vous sommant d’éclaircir ce mystère.
Parmi toutes les vidéos consultées celle qui m’a le plus interpelé est celle trouvée sur un site d’automédication où ils donnent une « explication du phénomène ».
Oui, vous avez bien lu :
Cette démonstration géométrique découverte par un magicien amateur américain nommé Paul Curry en 1953 repose en fait sur une illusion d’optique. Il s’agît de découper plusieurs "faux triangles" selon un quadrillage de sorte que l’hypoténuse soit légèrement concave ou convexe. En d’autres termes le plus grand côté du triangle n’est pas droit mais cela ne se voit pas, le spectateur à l’impression que le rectangle a été découpé sur les lignes d’origine pourtant les rangées ont été réduites. Cette illusion permet de refaire une autre reconstitution des morceaux de sorte qu’un carré disparaisse.
Joli morceau d’anthologie non seulement pour le charabia mais pour le contenu…
Peut-être le rédacteur a-t-il été déjà victime d’un matheux facétieux qui s’amuse à démontrer que 64 = 65 en découpant un carré 8x8 en « vrais triangles » et « vrais trapèzes » qui se reconstituent en un rectangle 5x13 mais là il est vrai que les « hypoténuses » (pourtant bien droites) n’ont pas tout à fait la même pente et qu’il reste un petit trou en forme de parallélogramme difficile à voir.
|

|
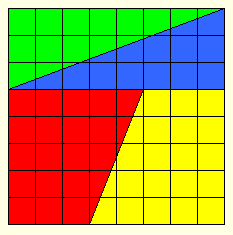
Mais ici rien de tel. Le couteau coupe bien droit des morceaux dont les côtés obliques ont tous la même pente et glissent sans problème les uns sur les autres. Mais alors d’où sort ce carré supplémentaire magique ?
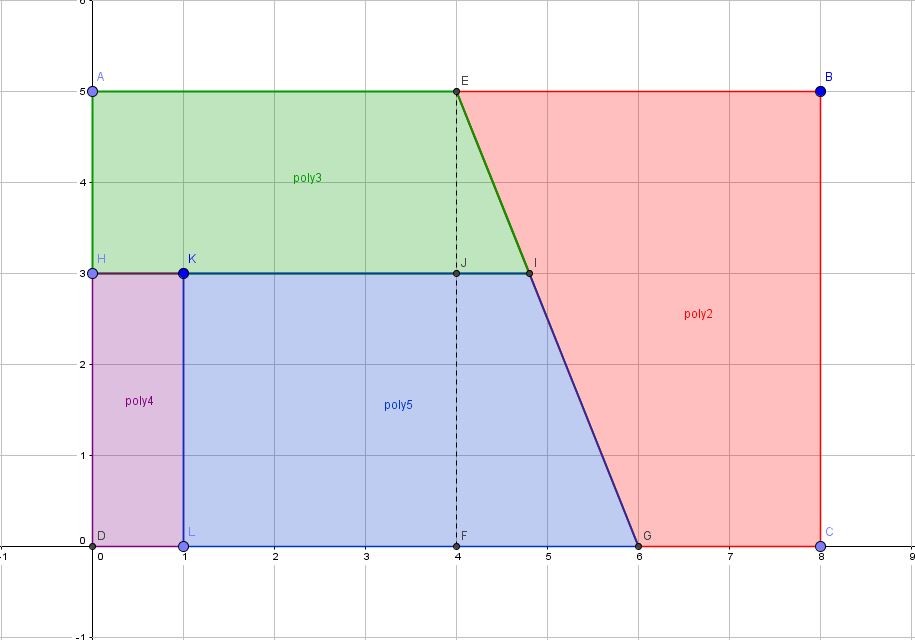
Un dessin soigné nous permet de le voir en utilisant un crayon à la place du couteau et du papier quadrillé en guise de chocolat.
|

|
On voit bien que toutes les pièces coïncident parfaitement mais que le rectangle initiale a diminué légèrement de longueur. Oh ! pas beaucoup : juste ce qu’il faut pour que cet $\epsilon \times 5 = 1$ donc $\epsilon = 0,2$. D’ailleurs puisque nous en sommes à faire des mathématiques, on vérifie dans le rectangle initial que pour la distance $KI$ (qui devrait valoir 4 pour venir en $K’E’$ reconstituer le rectangle de longueur 8), le compte n’y est pas. On peut demander à Thalès de calculer $JI$ puisque $ \dfrac{JI}{EJ} = \dfrac{FG}{EF}$ donc $=JI = 2\times\dfrac{2}{5} = 0,8$, juste le $\epsilon$ qui nous manquait.
Avec cette tablette de chocolat impossible de réitérer le processus. Mais avec une tablette plus sophistiquée (même si elle n’est plus en chocolat) on peut obtenir "un tour de magie" encore plus bluffant.
Nous avions déjà étudié il y a quelques années, dans les Chantiers 137, un autre tour de ce type appelé "puzzle de Sherlock Holmes" que vous pouvez télécharger ici (malheureusement le lien permettant de voir Bernard Bilis en action ne fonctionne plus).
Quelle place peut occuper dans nos classes de semblables "tour de magie" ? De la surprise à coup sûr, de la motivation pour faire des maths autrement, c’est certain. Comment le mettre en œuvre dans les classes : c’est cela que l’on appelle la pédagogie…
La Régionale Île-de-France APMEP, 26 rue Duméril, 75013 PARIS


