
Avis de recherche du n°192
Rappelons l’avis de recherche du numéro 192 d’avril 2022 :
Considérons l’entier $N$ = 123 456 789 et posons $U_N$ = 123 456 789 + 12 345 678 + 1 234 567 + 123 456 + 12 345 + 1 234 + 123 + 12 + 1 = 137 174 205, obtenu en ajoutant tous les entiers composés à partir des chiffres de $N$ en retirant successivement les chiffres des unités de l’entier précédent.
On pose aussi $S_N$ = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, qui est la somme des chiffres de $N$.
Il existe bien sûr une infinité de réels $p$ et $q$ tels que $U_N = pN + qS_N$,
mais il existe en particulier un couple $(p ; q)$, indépendant de $N$, pour lequel l’égalité $U_N = pN + qS_N$ est vraie pour tout entier positif $N$.
Sauriez-vous trouver un tel couple $(p \, { ;} \, q)$ ?
Voici une solution à cet avis.
Posons $N$ = $\sum\limits_{i=0}^n{a_i \times 10^i}$ .
On a donc $S(N)$ = $\sum\limits_{i=0}^n{a_i}$ et aussi, pour tout $k$ entre 0 et $n$, $E(\frac{N}{10^k})$ = $\sum\limits_{i=k}^n{a_i \times 10^{i-k}}$.
On a ainsi, pour $U(N)$ :
$U(N)$ = $\sum\limits_{k=0}^n{E(\frac{N}{10^k})}$ = $\sum\limits_{k=0}^n{\sum\limits_{i=k}^n a_i \times 10^{i-k}}$ = $\sum\limits_{k=0}^n{\left (a_k+10a_{k+1}+10^2a_{k+2}+ \cdots + 10^{n-k}a_n\right )}$
ce qui donne :
$U(N)$ = $(a_0+10a_1+10^2a_2+\cdots+10^na_n)$ + $(a_1+10a_2+10^2a_3+\cdots+10^{n-1}a_n)$ + $(a_2+10a_3+10^2a_4+\cdots+10^{n-2}a_n)$ + $\cdots$ + $(a_{n-1}+10a_n)$ + $a_n$
somme que l’on peut réorganiser :
$U(N)$ = $a_0$ + $(10 + 1)a_1$ + $(10^2+10+1)a_2$ + $\cdots$ + $(10^n+10^{n-1}+\cdots+1)a_n$
Or, pour tout $k$ entre 0 et $n$, $10^k + 10^{k-1} + \cdots + 1$ = $\dfrac{10^{k+1}-1}{9}$ (somme de termes de suite géométrique),
donc $U(N)$ = $\sum\limits_{k=0}^n{\dfrac{10^{k+1}-1}{9}a_k}$ = $\dfrac{10}{9}\sum\limits_{k=0}^n{10^ka_k} - \dfrac{1}{9}\sum\limits_{k=0}^n {a_k}$ = $\dfrac{10}{9}N - \dfrac{1}{9}S(N)$
Donc $p$ = $\dfrac{10}{9}$ et q = $-\dfrac{1}{9}$.
En particulier, $\dfrac{10}{9} \times 123\,456\,789 - \dfrac{1}{9} \times 45$ = $\dfrac{1\,234\,567\,845}{9}$ = $137\,174\,205$
Nouvel avis de recherche
Un exercice de recherche pas trop difficile, pour les vacances :
$ABCD$ est un rectangle. Le point $E$ est sur $[AB]$. $F$ est le point d’intersection de $[CE]$ et $[BD]$.
On définit ainsi cinq surfaces.
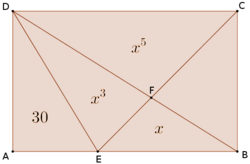
Si on note $x$ l’aire du triangle $BEF$, alors les aires des triangles $DEF$ et $CDF$ sont respectivement $x^3$ et $x^5$.
Par ailleurs, l’aire du triangle $ADE$ est 30.
Déterminer $x$, ainsi que l’aire du rectangle.
Question ouverte : les dimensions du rectangle sont-elles uniques ?
Pour cet avis de recherche, ainsi que des compléments sur des avis précédents, écrivez-nous à l’adresse des problèmes des Chantiers.
La Régionale Île-de-France APMEP, 26 rue Duméril, 75013 PARIS

