Solution de l’avis de recherche n°3

Soit $K(n,m)$ ce nombre cherché.

Conjecture initiale $(R)$ : on peut se contenter de chercher les cas où $m$ et $n$ sont premiers entre eux car sinon $K(n,m) = K(n’d,m’d) = K(n’,m’)$ où $d = PGCD(n,m)$ et dans ce cas $n’$ et $m’$ sont premiers entre eux.

Recherche expérimentale

Visiblement ici $K(1,m) = m$


Donc les valeurs obtenues sont $({\color{red} 1}, 2, 3, 4, 5, 6 …)$

Si $m = 2k$ alors $K(2,m) = k$

Si $m = 2k+1$ alors $K(2,m) = k+2$


Donc les valeurs obtenues sont $({\color{red} 1,\color{red} 3}, 2, 4, 3, 5, 4, 6, …)$

Si $m = 3k$ alors $K(3,m) = k$

Si $m = 3k+1$ alors $K(3,m) = k+3$

Si $m = 3k+2$ alors$ K(3,m) = k+3$


Donc les valeurs obtenues sont $({\color{red} 1,\color{red} 4,\color{red} 4}, 2, 5, 5, 3, 6, 6, …)$

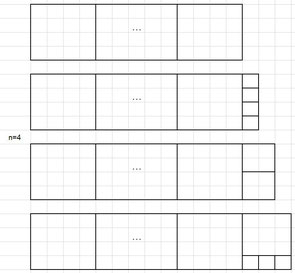
Si $m = 4k$ alors $K(4,m) = k$

Si $m = 4k+1$ alors $(4,m) = k+4$

Si $m = 4k+2$ alors$K(4,m) = k+2$

Si $m = 4k+3$ alors $K(4,m) = k+4$


Donc les valeurs obtenues sont $({\color{red} 1,\color{red} 5,\color{red} 3,\color{red} 5}, 2, 6, 4, 6, 3, 7, 5, 7 …)$

Il semblerait donc qu’il suffise de prendre le maximum de carrés de côté $n$ (i.e. en prendre $k = ent(m/n)$ ) et ensuite de trouver la solution pour $K(r,n)$ avec $r= m-kn$.

Malheureusement...

Si pour $m = 5k$ on obtient bien $K(5,m) = k$, pour $m = 5k+1$ les problèmes arrivent.

La méthode utilisée jusqu’à présent nous donne $K(5,m) = k+5$

Alors qu’en utilisant un carré de côté 5 de moins, le rectangle 5x6 peut être pavé par 5 carrés ce qui nous donne $K(5,m) = k-1+5 = k+4$

Donc à partir de maintenant nous allons changer de méthode en retirant $k-1$ grands carrés de côté $n$ (il semble impossible de faire mieux en retirant $k-2$ grands carrés mais je n’ai pas trouvé de démonstration satisfaisante : il s’agit donc d’une seconde conjecture $(R’)$ qui devra être démontrée ou infirmée par un contre-exemple) et ensuite nous examinerons uniquement les rectangles $ n \times m$ avec $n \lt m \lt 2n$.

Pour ce faire nous utiliserons la méthode $H(i)$ consistant à utiliser le maximum de carrés de côté $i$ pour $i \in [1,n]$.

$H(n)$ étant ce que nous faisions jusqu’à présent (puisque nous essayons de placer un grand carré de coté $ \gt n$) et $H(1)$ fournissant la plus mauvaise solution $m \times n$.

Essayons avec $n = 5$ et $m = 6$

Donc nous avons $K(5,6) = 5$

Et nous pouvons en tirer quelques conclusions. Le meilleur résultat est obtenu pour $i \gt \dfrac{n}{2}$ et il semble qu’en dessous les résultats soient plus mauvais et notamment pour $i = 1$ ou $i = 2$ qui obtiennent de très mauvais scores. cela reste à confirmer.

D’autre part le bon résultat de 3 est dû au fait que ce soit un diviseur de $m$ et qu’en plus $n-3=2$ et que l’on puisse paver l’espace restant avec 3 carrés de côté 2. Sans pouvoir en tirer une règle il conviendra de faire plus attention au cas où $i$ est un "grand" diviseur de $n$ ou $m$.

Examinons les autres rectangles de largeur 5 :

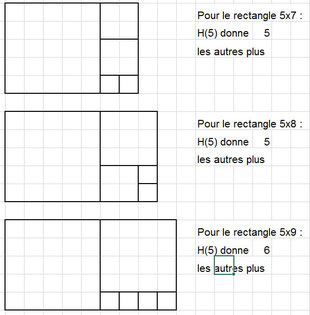
Nous examinons tous les autres rectangles de largeur 5 et de longueur 7, 8 et 9.

À chaque fois c’est $H(5)$ qui donne la meilleure solution

Donc en résumé pour $K(5,m)$ nous obtenons :
$({\color{red}1,\color{red} 5,\color{red} 5,\color{red} 5,\color{red} 6}, 2, 6, 6, 6, 7, 3, 7, 7, 7, 8 ...)$

Explorons le cas $n = 6$

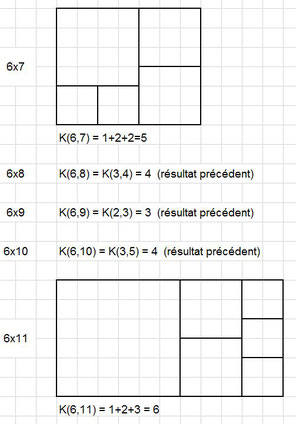
Ici 2 cas seulement à examiner car tous les autres sont donnés par des résultats déjà trouvés.

La méthode est toujours la même.

Par exemple pour 6×7

d’abord $H(6)$ qui donne $1+6=7$ puis $H(5)$ qui donne $1+3+5=9$

enfin $H(4)$ qui fournit la meilleure réponse car les suivants sont plus mauvais.

Donc pour $K(6,m)$ nous avons : $({\color{red}1,\color{red} 5,\color{red} 4,\color{red} 3,\color{red} 4,\color{red} 6}, 2, 6, 5, 4, 5, 7, 3 ,7, 6, 5, 6, 8 …)$

J’avais exploré beaucoup plus loin mais pas très loin quand même…

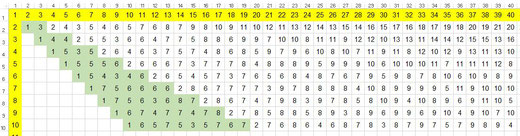
…quand un fidèle lecteur, Salvatore Tummarello, (qui cherchait de son côté et croyait avoir trouvé un algorithme fournissant le résultat mais qui ne fonctionnait pas pour 11×13), m’avertissait qu’il avait trouvé... sur internet (là où j’avais cherché désespérément mais en oubliant qu’on pouvait chercher aussi en anglais) un site étasunien qui s’intéressait à ce problème et qui semblait en avance sur nos recherches (pour rester modeste).

Notamment ils ont eu le mauvais goût de trouver un contre-exemple à ma conjecture selon laquelle il suffisait de chercher pour $n \lt m \lt 2n$ et d’ajouter autant de fois que nécessaire le nombre de carré de côté $n$. Évidemment il fallait aller chercher un peu plus loin puisqu’ils avaient montré que $K(112,53) = K(59,53)$ alors que $112=59+53$ ! Voici la preuve irréfutable :

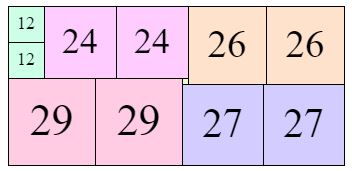
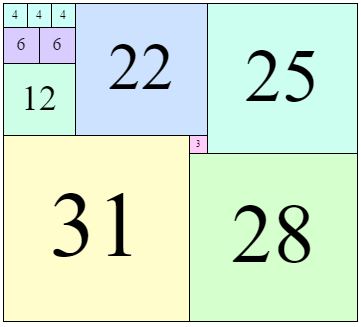
Ils ont aussi mis au point une "machine" à fournir les résultats mais jusqu’à $n=350$ seulement pour l’instant ! (ce qui m’a permis de constater avec satisfaction que je trouvais, avec ma méthode artisanale, les mêmes résultats qu’eux... jusqu’à $n=10$).

Quant à savoir comment ils avaient fait et si leurs résultats étaient exacts je ne peux que vous inviter à aller le vérifier vous-mêmes en visitant leur site.

Si quelque spécialiste du C++ pouvait s’y plonger et nous expliquer…

Avis de Recherche n° 4