Le critère de Chika
Pendant sa scolarité l’élève apprend les critères de divisibilité classiques par 2 ; 3 ; 5 ; 9 et 10. Parfois on y ajoute les critères de divisibilité par 4 ; par 6 et par 11. La question légitime qu’un élève curieux peut alors se poser est : comment fait-on pour 7 et 8 ?
Là, la réponse que l’on peut donner, pourrait clore tout débat et ramener les élèves aux critères classiques vus en cours, comme elle pourrait s’ouvrir sur un débat et amener les élèves à faire des recherches en laissant la question ouverte. Du point de vue pédagogique, il est plus intéressant d’amener les élèves sur un terrain dans lequel ils (se) posent de nouvelles questions et de leur laisser le temps de faire des recherches et peut-être de faire des découvertes originales ou pas !

C’est ce qui est arrivé, en 2019 au jeune élève de 12 ans, Chika Ofili vivant au Royaume-Uni. Avant de partir en vacances, sa professeure de mathématiques Mary Ellis lui avait prêté un live de mathématiques (’’First Steps for Problem Solvers’’ de Mary Teresa Fyfe et Andrew Jobbings, 2016).
Dans ce livre, le jeune Chika a trouvé les critères de divisibilité classiques mais il n’a pas trouvé celui de 7. Il s’est penché alors sur le problème et au retour des vacances il est revenu avec la solution ! Cette découverte lui a valu un prix lors de la cérémonie « TruLittle Hero awards 2019 » qui récompense les réalisations exceptionnelles d’enfants de moins de 17 ans.
Avant de découvrir la solution apportée par Chika, une chose est sûre, le jeune Chika a bien cherché la solution du problème. L’a-t-il réellement découverte par lui même ou bien l’a-t-il trouvée sur internet ?
En cherchant un peu sur internet, et sans aller sur des sites spécialisés, on découvre que la réponse apportée par Chika existe déjà. En effet, une vidéo en anglais faite par un « youtubeur » indien et datant de juillet 2017 explique en détail la même solution apportée par Chika deux ans plus tard.
Dans ce qui suit nous allons découvrir et démontrer la solution apportée par Chika et voir comment la généraliser à d’autres nombres et obtenir d’autres versions des critères de divisibilité classiques.
Le critère de divisibilité par 7
Pour bien comprendre comment cela marche, commençons par un exemple. Prenons le nombre 1 329. Pour savoir si ce nombre est divisible par 7 on multiplie le chiffre des unités par 5 et on l’ajoute au nombre formé par les autres chiffres. On réitère cette méthode jusqu’à ce que l’on arrive à un nombre à deux chiffres dont la divisibilité par 7 est facile à vérifier. On obtient ainsi un algorithme que l’on pourrait travailler avec les élèves en séance d’algorithmique débranchée ou sur un logiciel de programmation.
Dans notre exemple, calculons : 132 + 9×5 = 132 + 45 = 177.
Nous réitérons ce processus en calculant : 17 + 7×5 = 17 + 35 = 52.
Le nombre 52 n’est pas un multiple de 7. Par conséquent 1 329 n’est pas divisible par 7. Une simple vérification nous donne que le reste de la division de 1 329 par 7 est 6.
Prenons un autre exemple : 3 178
Calculons 317 + 8×5. On trouve 317 + 40 = 357.
À nouveau, calculons : 35 + 7×5 = 35 + 35 = 70. Ce qui implique que 3 178 est divisible par 7. Pour vérifier cette affirmation, un simple calcul à la main le confirmera.
Le Critère
Soit K un entier plus grand que 10. Soit U le chiffre des unités et L le nombre formé par les autres chiffres de K. On peut donc écrire K sous la forme K=L×10+U.Le critère de divisibilité par 7 consiste à dire que l’entier K est divisible par 7 si et seulement si L+5U l’est aussi.
Démonstration
En ajoutant à l’entier K un multiple de 7, la divisibilité de cette somme par 7 reste la même que celle de K. Ainsi, on peut dire que l’entier K est divisible par 7 si et seulement si K+49U l’est aussi.En remplaçant K par 10 L+U on obtient K+49 U = 10L+50U ce qui donne, en factorisant 10, 10×(L+5U). Puisque 10 n’est pas divisible par 7 alors on peut dire que K est divisible par 7 si et seulement si L+5U l’est aussi.
L’idée principale dans cette démonstration est de faire sortir 10 en facteur et ne laisser que L+5U qui est plus petit que le nombre K sauf dans un nombre fini de cas dans lesquels K < 49. En effet, L+5U > 10L+U si et seulement si 4U > 9L.
Remarque : Au début, au lieu d’ajouter 49U, on aurait pu ajouter (-3)×7U =-21U, ce qui aurait donné : K+(-21)U = 10L-20U = 10×(L-2U).
On obtient ainsi un autre critère de divisibilité par 7 : K est divisible par 7 si et seulement si L−2U l’est aussi. On peut aussi déduire ce dernier critère du premier en enlevant tout simplement 7U à L+5U.
En reprenant l’exemple de 1 329, nous avons L-2 U = 132−18 = 114.
Dans notre algorithme, K devient 114 et en réitérant le calcul on obtient L−2 U = 11−8 = 3. Ce dernier nombre n’est évidemment pas un multiple de 7.
Dans le deuxième exemple de 3 178, nous avons L-2 U = 317−16 = 301.
Dans notre algorithme, K devient 301 et en réitérant le calcul on obtient L-2 U = 30−2 = 28. Ce dernier nombre est évidemment un multiple de 7.
Généralisation de cet algorithme à d’autres nombres
Cette démonstration nous suggère de reprendre l’idée et de l’essayer pour les cas classiques de divisibilité par 3, 5 et 9 et d’autres entiers impairs.
Divisibilité par 3
Nous savons que 3×3 = 9, le nombre K+9U est de même nature que K quant à sa divisibilité par 3.
L’entier K+9U = 10L+U+9U = 10(L+U). Puisque 10 n’est pas un multiple de 3, on peut dire que K est divisible par 3 si et seulement si L+U l’est aussi.
Exemple : vérifier si 41 752 est divisible par 3 revient à faire cette vérification aux nombres :
4 175+2 = 4 177 ; 417+7 = 424 ; 42+4 = 46 et 4+6 = 10.
Remarque : Au début, au lieu d’ajouter 9U, on aurait pu ajouter (-7)×3U = -21U, ce qui aurait donné : K +(-21)U = 10L-20U = 10×(L-2U).
On obtient ainsi un autre critère de divisibilité par 3 : K est divisible par 3 si et seulement si L−2U l’est aussi. On obtient ainsi un critère identique au deuxième critère de divisibilité par 7.
En reprenant l’exemple de K = 4 1752 l’entier L-2U = 4 175 - 2×2 = 4 171.
Dans notre algorithme K devient 4 171 et L-2U = 417−2×1 = 415.
À nouveau K devient 415 et L-2U = 41−2×5 = 31. Ce dernier n’est évidemment pas un multiple de 3.
À chaque étape on peut, évidemment, utiliser l’un des deux critères. La somme reste la plus simple pour l’élève.
Divisibilité par 5
Même si le cas de 5 est évident, l’idée d’ajouter un multiple de 5 à K pour obtenir un multiple de 10 ne fonctionne que si U est égal à 0 ou à 5. Dans ces deux cas seulement l’entier K est divisible par 5.
Divisibilité par 9
La même démonstration que pour le cas de 3 marche aussi pour le cas du 9. Ainsi on peut dire que K est divisible par 9 si et seulement si L+U l’est aussi.
Remarque : Au début, au lieu d’ajouter 9U, on aurait pu ajouter (-9)×9U = -81U, ce qui aurait donné : K+(−81)U = 10L−80U = 10×(L−8U).
On obtient ainsi un autre critère de divisibilité par 9 : K est divisible par 9 si et seulement si L−8U l’est aussi.
Divisibilité par 11
Nous savons que 11×(−1) = −11, le nombre K+(-11)U est de même nature que K quant à sa divisibilité par 11.
Le nombre K +(-11)U = 10 L + U − 11U = 10(L-U). Puisque 10 n’est pas un multiple de 11, on peut dire que K est divisible par 11 si et seulement si L−U l’est aussi. Ce critère est très simple à retenir pour les élèves.
Exemple : Prenons K = 28 416. Dans ce cas L−U = 2 841−6 = 2 835.
Dans notre algorithme K devient 2 835 et à nouveau L−U = 283−5 = 278.
K devient 278 et L−U = 27−8 = 19. On peut s’arrêter là et conclure la non divisibilité par 11 de tous ces nombres K dans l’algorithme. Si l’on continue, K devient 19 et L−U = 1−9 = −8.
Prenons un 2e exemple d’un nombre divisible par 11 ; prenons 11×439 = 4 829.
K = 4 829 et le nombre K devient 473 et L−U = 482−9 = 473.
L−U = 47−3 = 44. Ce dernier est bien divisible par 11.
Remarque : En ajoutant 11U à L−U nous obtenons un 2e critère : K est divisible par 11 si et seulement si L+10U l’est aussi.
Dans l’exemple K = 4 829, le nombre L+10U = 482+90 = 572. Nous réitérons le processus, l’entier K devient 572 et L+10U = 57+20 = 77 qui est évidemment un multiple de 11.
Divisibilité par 13
Nous savons que 3×13 = 39, le nombre K+39U est de même nature que K quant à sa divisibilité par 13. L’entier K+39 U = 10L+U+39U = 10(L+4U). Puisque 10 n’est pas un multiple de 13, on peut dire que K est divisible par 13 si et seulement si L+4U l’est aussi.
En enlevant 13U à ce dernier nous obtenons un 2e critère : K est divisible par 13 si et seulement si L−9U l’est aussi. Le premier critère avec l’addition reste plus pratique pour un calcul mental.
Exemple : Prenons le nombre K = 13×152 = 1 976. Dans ce cas L+4U = 197 + 4×6 = 197+24 = 221. K devient alors 221 et L+4U = 22+4×1 = 26. Ce dernier est évidemment divisible par 13.
Divisibilité par 17
Nous savons que 7×17 = 119, le nombre K+119U est de même nature que K quant à sa divisibilité par 17. L’entier K+119U = 10L+U+119U = 10 (L+12U). Puisque 10 n’est pas un multiple de 17, on peut dire que K est divisible par 17 si et seulement si L+12U l’est aussi.
En enlevant 17U à ce dernier nous obtenons un 2e critère : K est divisible par 17 si et seulement si L-5U l’est aussi. Ce dernier critère est plus pratique pour un calcul mental.
Divisibilité par 19
Le nombre K+19U est de même nature que K quant à sa divisibilité par 19. L’entier K+19U = 10L+U+19U = 10(L+2U). Puisque 10 n’est pas un multiple de 19, on peut dire que K est divisible par 19 si et seulement si L+2U l’est aussi.
Divisibilité par 21
Bien sûr pour tester la divisibilité d’un nombre par 21 il suffit de tester sa divisibilité par 7 et 3. Il se trouve que pour ces deux nombres nous avons un critère « commun » qui passe par le calcul de L-2U (voir les démonstration correspondantes). Le nombre K est donc divisible par 21 si et seulement si L-2U l’est aussi.
Divisibilité par 23
Le nombre K+3×23U = K+69U est de même nature que K quant à sa divisibilité par 23. L’entier K+69U = 10L+U+69U = 10(L+7U). Puisque 10 n’est pas un multiple de 23, on peut dire que K est divisible par 23 si et seulement si L+7U l’est aussi.
Récapitulatif
Soit K un entier, U son chiffre des unités et L le nombre formé par les autres chiffres. Le tableau ci-dessous donne les critères de divisibilité par les nombres que l’on a vus dans cet article.
| Divisibilité de K par | 3 | 7 | 9 | 11 | 13 | 17 | 19 | 21 | 23 |
| Division à tester | L+U | L+5U | L+U | L-U | L+4U | L-5U | L+2U | L-2U | L+7U |
| L-2U | L-2U | L-8U | L-10U | L-9U | L+12U | L-17U | L+19U | L-16U |
Pour les quatre dernières cellules, les critères correspondant ne sont pas pratiques pour un calcul mental.
Bonus !
Nous venons de décrire une méthode simple et efficace pour trouver les critères de divisibilité par n’importe quel nombre impair qui ne se termine pas par 5 (en particulier n’importe quel nombre premier autre que 5) . Selon le chiffre des unités du diviseur, nous additionnons, au nombre à tester, un multiple bien choisi du diviseur.
Nous laissons le lecteur trouver les critères de divisibilité par 27, 29 et 31 et d’autres entiers impairs s’il le veut. Des critères communs peuvent exister et d’autres liens intéressants peuvent apparaître, donnant lieu à des règles et peut-être bien à des conjectures pour les élèves curieux (observez bien les critères de divisibilité par 9, 19, 29, … ; ceux de 11, 21, 31, … ; ceux de 3, 13, 23, … ; ceux de 7, 17, 27, ...). Au lecteur de les trouver !
Divisibilité par 8 et 4
Pour finir nous donnons le critère de divisibilité par 8 évoqué au début de l’article, et au passage le critère de divisibilité par 4. Ainsi, le lecteur aura tous les critères de divisibilité par les premiers entiers jusqu’à 10.
Soit K un entier pair quelconque. Écrivons K sous la forme Mcdu où u est le chiffre des unités, d le chiffre des dizaines et c le chiffre des centaines. M est le nombre formé par le reste des chiffres à partir des milliers. Nous pouvons donc écrire K = M×1 000+c×100+d×10+u. Nous savons que 1 000 = 8×125 ; 100 = 8×12 + 4 et 10 = 8+2. Le nombre K peut donc s’écrire sous la forme K = 8×(125M+12c+d)+4c+2d+u.
Le nombre K est donc divisible par 8 si et seulement si 4c+2d+u l’est aussi. Ceci équivaut à dire que le nombre 2c+d+$\frac{u}{2}$ est un multiple de 4 ou encore 2c+d+$\frac{u}{2}$+8c est un multiple de 4. Ce qui revient à dire que le nombre 10c+d+$\frac{u}{2}$ est un multiple de 4.
Or le nombre 10c+d+$\frac{u}{2}$ n’est autre que le nombre cd formé par les deux chiffres c et d auquel on a ajouté $\frac{u}{2}$.
Donc K = Mcdu est divisible par 8 si et seulement si cd+$\frac{u}{2}$ est divisible par 4.
Exemple : Prenons K = 215 996. Pour voir si ce nombre est divisible par 8 il suffit de vérifier si 99+6/2 = 102 est divisible par 4. Ce qui n’est pas le cas ici car le nombre 02 formé par les deux premiers chiffres 0 et 2 n’est pas un multiple de 4.
Remarque : En suivant le même principe de la démonstration précédente nous pouvons montrer qu’un nombre pair K= Mcdu est divisible par 4 si et seulement si d+$\frac{u}{2}$ est pair.
Le nombre K de l’exemple précédent est divisible par 4 car 9+6/2 = 12.
Algorithmique
En classe j’ai abordé le critère de Chika avec mes élèves de 3e et je leur ai demandé de programmer l’algorithme de Chika sur Scratch. Le but de cette partie est d’exploiter les travaux des élèves pour aiguiser leur esprit critique.
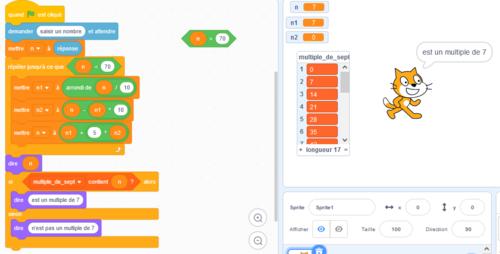
Voici deux programmes faits par deux élèves, le premier celui de Yanis et le deuxième celui de Quentin.
Les deux programmes fonctionnent bien mais en les analysant de plus près on se rend compte qu’ils ont quelques petits problèmes.
Dans le premier programme, pour déterminer le nombre formé par tous les chiffres à partir des dizaines, Yanis prend la valeur arrondie à l’unité du quotient du nombre de départ par 10.
Dans l’exemple de la figure, le nombre de départ est 749. Ce nombre est évidemment divisible par 7. Si l’on suit le programme de Yanis. Le programme calcule d’abord le quotient 749÷10 = 74,9 puis il arrondit à 75. Le programme calcule ensuite la différence 749−75×10 = −1. Le programme calcule ensuite la somme 75+5×(−1) = 70 et réactualise le nombre de départ à 70.
Le programme de Yanis réitère ce procédé au nouveau nombre 70 qu’il réactualisera à la fin à 7. Avec ce procédé, le programme n’applique pas exactement le critère de Chika mais donne un résultat juste qu’on peut même le démontrer. Ce n’était pas l’intention de l’élève.
Autre chose, le programme de Yanis accepte les nombres décimaux en entrée et annonce à la fin que le nombre n’est pas divisible par 7 mais pour une autre raison propre au fonctionnement de scratch qui fait la différence entre par exemple 14 et 14,00.
Pour mieux illustrer ce problème appliquons le programme de Yanis au nombre 753,2 qui est évidemment décimal. Le programme calcule d’abord 753,2÷10 = 75,32 et arrondit le résultat à 75. Le programme calcule ensuite la différence 753,2−75×10 = 3,2 . Pour le programme 3,2 est le « chiffre des unités », ce qui est faux. Le programme calcule ensuite la somme 75+3,2×5 = 75+16,00 = 91,00.
Le programme de Yanis réitère ce procédé au nouveau nombre 91,00. Le programme calcule alors 91,00÷10 = 9,10 et arrondit le résultat à 9 qui est le chiffre des dizaines. Le programme calcule ensuite la différence 91,00−9×10 = 01,00 pour trouver le chiffre des unités. Le programme calcule ensuite la somme 9+1,00×5 = 14,00. Le programme vérifie ensuite si 14,00 est dans la (liste) table de multiplication de 7.
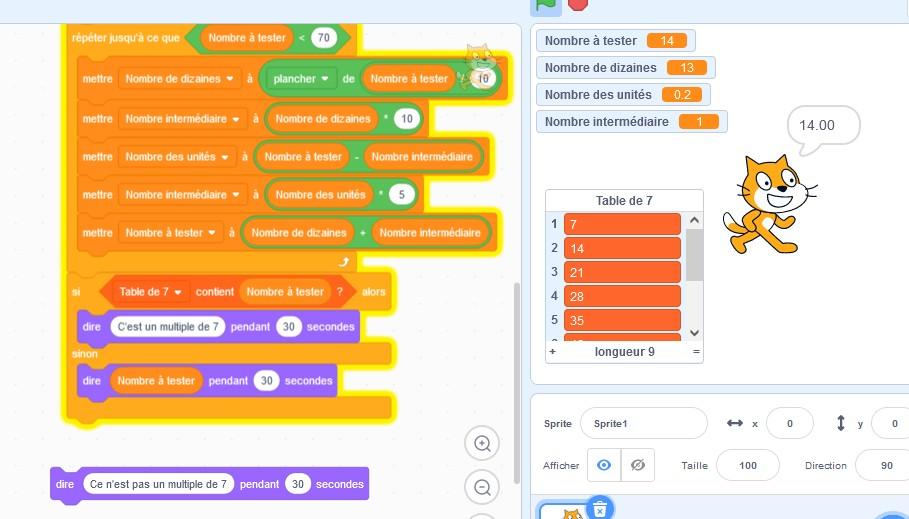
Malgré le fait que 14 soit bien dans la liste, le logiciel ne reconnaît pas l’égalité 14 = 14,00 et annonce alors que le nombre 753,2 n’est pas divisible par 7, voir la figure suivante :
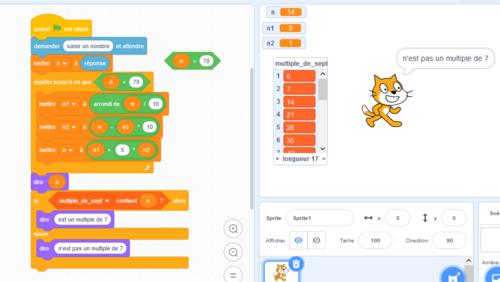
Pour comprendre ce qui s’est passé j’ai modifié le programme de Yanis pour afficher le nombre de départ « n » actualisé à la fin de la boucle finie. Voici la valeur affichée par Scratch :
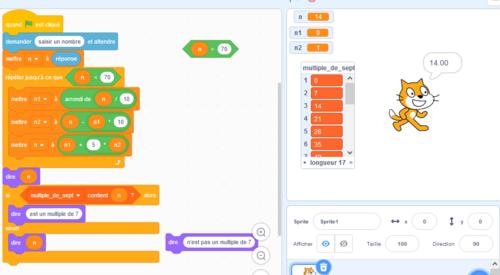
Le programme de Quentin n’a pas de problème d’arrondi mais il accepte les nombres décimaux et il a le même problème que celui de Yanis. Voici ce qu’affiche le programme de Quentin appliqué au nombre 130,2 :
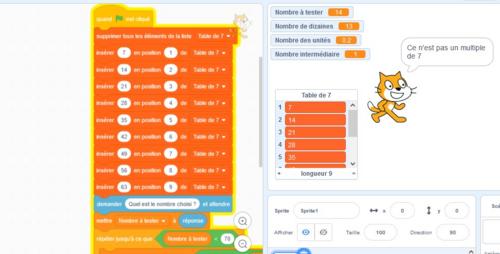
Le nombre réactualisé à la fin du programme est bien 14,00 mais le programme annonce que ce dernier n’est pas divisible par 7 pour la même raison ( 14 ≠ 14,00 pour scratch !). Ceci pourrait peut-être venir du type attribué en arrière plan au nombre 14 (integer) et à 14,00 (float).
La Régionale Île-de-France APMEP, 26 rue Duméril, 75013 PARIS