Une nouvelle approche
Le but de cet article est de définir une nouvelle approche géométrique et pédagogique pour faire les opérations sur les fractions. Cette approche provient de la construction, connue en algèbre, de l’ensemble des nombres rationnels $\mathbb{Q}$ à partir du réseau $\mathbb{Z}$×$\mathbb{Z^*}$. Pour rester au niveau collège, on se limitera à des termes simples compréhensibles par les élèves. Cette nouvelle approche fera aussi intervenir les transformations géométriques enseignées au collège (symétries axiale et centrale, translations, rotations et homothéties) ce qui mettra en lumière la belle harmonie qui existe entre l’algèbre et la géométrie.
Le travail présenté ici aboutit finalement à la description d’un nouvel instrument que j’appellerais « Fractiomètre » ou « Fractiolabe ». Celui-ci permettra de faire du calcul fractionnaire et même plus comme par exemple l’estimation rapide d’un produit (en particulier une aire rectangulaire), d’une racine carrée ou les racines d’un polynôme du 2nd degré, tout cela sans avoir recours à des calculs.
Les rectangles élastiques posés
Tout le monde connaît les télévisions de format « seize neuvième » et s’accorde à dire que le rapport entre la base et la hauteur est toujours égal à cette fraction quelle que soit la taille de la télévision. Ainsi la fraction $16 \over 9$ caractérise cette famille (une classe d’équivalence) de télévisions similaires tout comme la fraction $\frac{4}{3}$ qui caractérisait l’ancienne génération de télévisions.
Malgré la forme rectangulaire de la télévision, on parlera dans cet article de base (côté sur lequel repose la télévision) et de hauteur au lieu de parler de longueur et de largeur. En effet, on distinguera un même rectangle posé horizontalement sur sa longueur ou sur sa largeur. On parlera donc de rectangles posés ayant une base et une hauteur. Puisqu’un rectangle a une famille infinie de rectangles similaires posés (par agrandissement ou réduction), on parlera, dans ce sens, de « rectangles élastiques posés ».
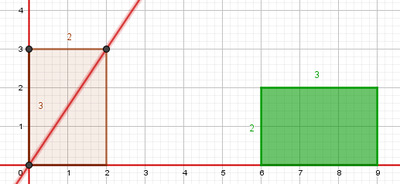
À chaque fraction (et par extension à chaque nombre en écriture fractionnaire) $\dfrac{x}{y}$, on associe dans le plan, muni d’un repère orthonormé, un rectangle posé $ABCD$ de base $[AB]$ de longueur $x$ et de hauteur $[AD]$ de longueur $y$. Dans la notation $ABCD$, on supposera que $A$ et $B$ sont deux points de l’axe des abscisses avec l’abscisse de $A$ inférieure à celle de $B$. Puisque la lecture se fait dans le sens direct (sens inverse des aiguilles d’une montre), on appellera $A$ l’origine du rectangle posé, $B$ le point base, $C$ le sommet principal et $D$ le point hauteur.
Au passage, on note le lien qui existe entre les différentes combinaisons de $x$ et $y$ et les caractéristiques géométriques d’un rectangle (posé) : hormis la longueur et la largeur, la somme de $x$ et $y$ est le demi périmètre du rectangle, le produit $xy$ est l’aire du rectangle, $x^2+y^2$ est le carré de la diagonale et le rapport $\dfrac{x}{y}$ est la tangente de l’angle entre la diagonale du rectangle et sa hauteur. La partie entière de ce rapport $\dfrac{x}{y}$ représente aussi le nombre de carrés de côté $y$ contenus dans le rectangle.
Ainsi l’aire du rectangle est égale au produit de l’aire du carré de côté $y$ par la tangente de l’angle entre la diagonale du rectangle et sa hauteur, soit $y^2 \times {\dfrac{x}{y}}=xy$ .
Les nombres en écriture fractionnaire $\dfrac{k \times x}{k \times y}$, où $k$ est un nombre non nul (dont la nature est à spécifier selon l’étude : entier naturel ou relatif, ...) définissent ces rectangles posés semblables de bases $k \times x$ et de hauteur $k \times y$.
En faisant des translations horizontales des rectangles posés le long de l’axe des abscisses pour ramener leur origine $A$ sur l’origine du repère $O$, les diagonales issues de $O$ sont sur la droite $(OC)$, voir la Figure 1 ci-dessous. Ainsi, la diagonale d’un rectangle posé issue de $O$ définit tous ses rectangles semblables, à une translation horizontale près. Pour simplifier, on parlera de diagonale principale.

La diagonale issue de $O$ est commune aux trois rectangles.
Ainsi, les fractions égales correspondent à une seule famille de rectangles similaires posés. Cela permettra donc de faire géométriquement :
- la simplification des fractions,
- la recherche de la quatrième proportionnelle,
- et le test d’égalité entre les nombres en écriture fractionnaire.
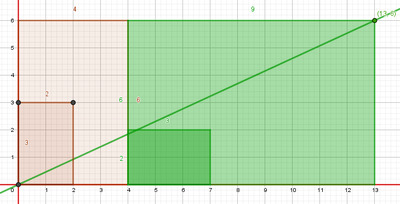
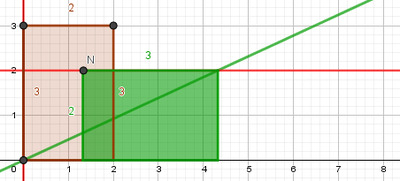
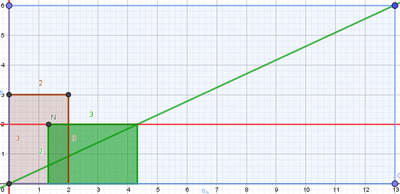
Pour aborder les cas où $k$, $x$ ou $y$ sont négatifs on élargira le principe aux rectangles posés de bases ou de hauteurs négatives (vues comme mesures algébriques). Ainsi, dans la même classe des rectangles posés décrits par l’exemple de la Figure 1, on trouvera des rectangles posés dans le 3e quadrant du plan. Les Figures 2 et 3 suivantes donnent des exemples de rectangles posés de même classe correspondant à des nombres rationnels positifs ou négatifs.
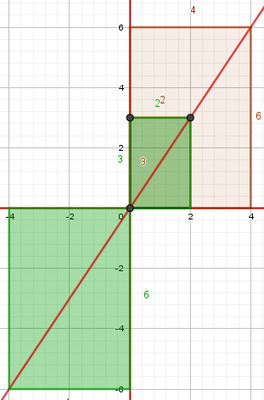
Figure 2 : Rectangles posés « positifs »
représentant le nombre rationnel $\frac{-2}{-3}$ |

Figure 3 : Rectangles posés « négatifs »
représentant le nombre rationnel négatif $\frac{-2}{3}$ |
Estimation de la valeur décimale d’une fraction
Dans chaque classe de rectangles posés, il existe un représentant de hauteur $1$ et un autre de hauteur $10$. Ces représentants correspondent, en général, à des nombres en écriture fractionnaire.
L’intersection de la diagonale principale avec les droites horizontales d’équations $y=1$ et $y=10$ nous donne, par lecture graphique, une estimation rapide de la valeur décimale de la fraction.
L’intersection avec la droite d’équation $y=10$, nous donne une lecture plus précise que celle avec la droite d’équation $y=1$. Sur la Figure 4 ci-contre, on donne un exemple d’estimation par lecture graphique de la valeur décimale d’une fraction.
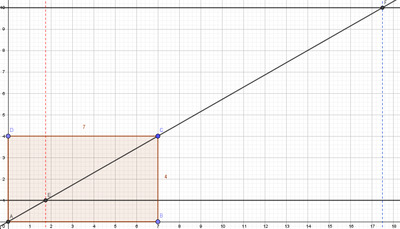
La diagonale principale du rectangle posé de base $7$ et de hauteur $4$ coupe la droite d’équation $y=1$ en un point $E$ dont l’abscisse semble être proche de $1,8$. L’intersection avec la droite d’équation $y=10$ donne un point F dont l’abscisse semble être juste au milieu entre $17,4$ et $17,6$, c’est à dire $17,5$. Par conséquent, on pourrait estimer la valeur de $\frac{7}{4}$ à $\frac{17,5}{10} $ = $1,75$.
Simplification d’une fraction
La notion de diagonale principale nous aide à simplifier géométriquement une fraction et à déterminer le pgcd [1] du numérateur et du dénominateur. Elle pourrait aussi nous donner une belle activité de passage de l’arithmétique au théorème de Thalès. On prend, par exemple, la fraction $15 \over 10$. On trace le rectangle posé associé à cette fraction ainsi que sa diagonale principale, voir Figure 5 ci-dessous.

Le premier point d’entre eux à partir de l’origine donne la fraction irréductible $\frac{3}{2}$ égale à $\frac{15}{10}$.
Géométriquement, la fraction irréductible associée à $15 \over 10$ correspond au premier point de coordonnées entières, sur la diagonale principale, proche de l’origine du repère. La lecture graphique nous donne le point $E(3 ; 2)$ et donc la fraction réduite $3 \over 2$.
Les points $E$, $F$, $G$, $H$ de coordonnées entières partagent la diagonale principale $[AC]$ en $5$ intervalles de même longueur. Le nombre d’intervalles détermine alors le plus grand diviseur commun de $15$ et $10$. Ainsi, on pourra partager chacun des côtés $[AB]$ et $[BC]$ en $5$ intervalles de même longueur. Plusieurs configurations de Thalès peuvent être déduites ainsi que les rapports correspondants, voir Figure 6 ci-dessous.
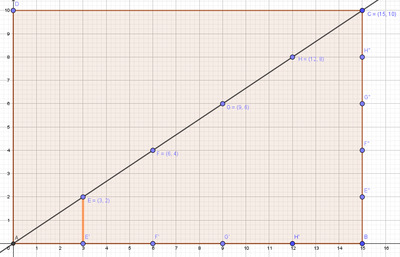
Plusieurs configurations de Thalès peuvent être mises en évidence et exploitées en cours.
Addition de deux fractions
Pour illustrer géométriquement l’addition de deux fractions, on représente chaque fraction par son rectangle posé. On a maintenant deux façons de faire.
On cherche dans chaque classe d’équivalence un représentant ayant la même hauteur (entière) que celui de l’autre classe. L’addition se fait alors par la fusion des deux rectangles le long de leur hauteur. Les Figures 8 à 10 ci-dessous illustrent l’addition ${3 \over 2} +{ 5 \over 4}$.
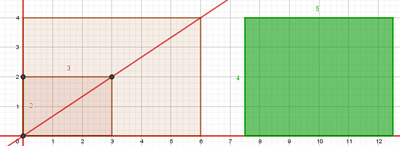
Sa base mesure $6$ (unités).

du nouveau rectangle posé donnant le résultat $\frac{11}{4}$
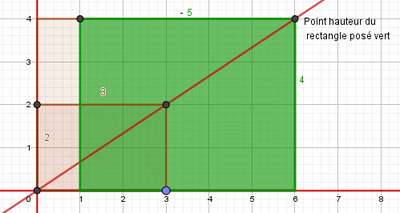
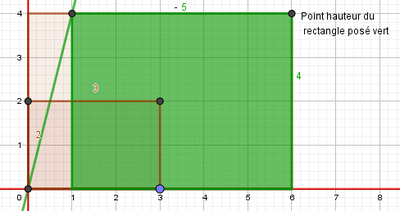
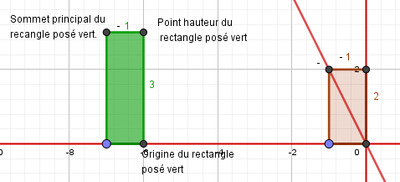
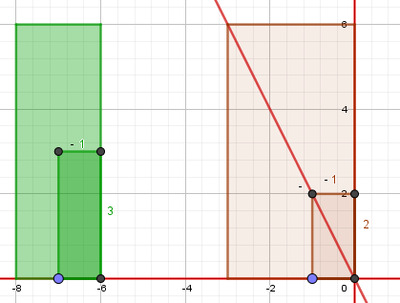
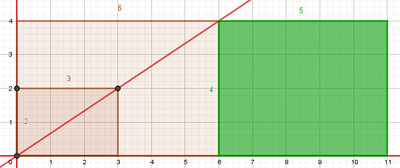
On trace, à partir de l’origine, le rectangle posé représentant la fraction $3 \over 2$ ainsi que sa diagonale principale. On trace ensuite le rectangle posé représentant la fraction $5 \over 4$. On translate ce dernier horizontalement jusqu’à ce que son point hauteur (sa hauteur gauche) touche la diagonale principale du premier rectangle comme sur les Figures 11 et 12 ci-dessous.
À droite, rectangle posé représentant la fraction $\frac{5}{4}$.

au contact de la diagonale principale du rectangle marron.
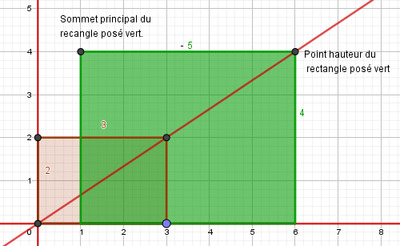
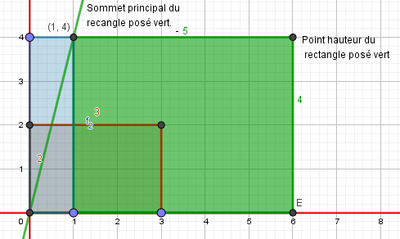
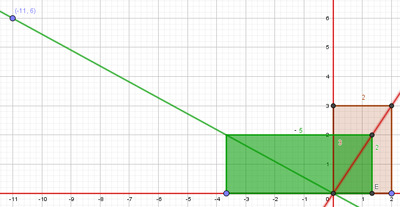
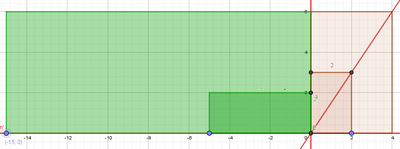
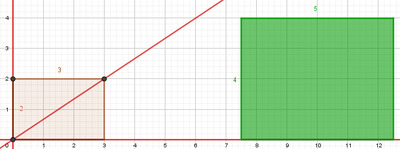
Dans cette position, on trace la nouvelle diagonale principale reliant $O$ au sommet principal (de coordonnées $(11 ; 4)$) du rectangle posé vert comme sur la Figure 13 ci-dessous.

Voici un autre exemple illustrant la somme de deux fractions dont les dénominateurs ne sont pas multiples l’un de l’autre, par exemple la somme ${2 \over 3} + {3 \over 2}$.
Soustraction des fractions
Pour simplifier les choses, on fera la soustraction on utilisant la règle de conversion en l’addition de l’opposé. On pourra aussi faire l’opération en tant qu’action de « soustraire » sur les rectangles posés.
Avec cette dernière action on se sera obligé de revenir avec les élèves sur le sens de soustraire un nombre négatif à un autre (positif ou négatif, de pus grande valeur absolue ou pas). Il y aura plusieurs cas à distinguer selon les situations.
Dans la suite on passera par la règle de l’addition de l’opposé et on ne rentrera pas dans la discussion liée à la soustraction des nombres relatifs.
On prend par exemple ${3 \over 2} - {5 \over 4}$ pour expliquer comment faire la soustraction en manipulant les rectangles posés.
On trace les rectangles posés correspondant à $3 \over 2$ et $5 \over 4$. Le rectangle posé correspondant à $5 \over 4$ doit se situer dans le 2ème cadran du plan, comme sur la Figure 21 ci-dessous. Dans cette situation, le sens de lecture du nom du rectangle $ABCD$ se fait dans le sens indirect. Le point $A$ reste toujours l’origine du rectangle mais il est situé complètement à droite, $B$ reste toujours le point base (sur l’axe des abscisses), C est toujours le sommet principal mais il se situe cette fois-ci à gauche du point hauteur $D$.
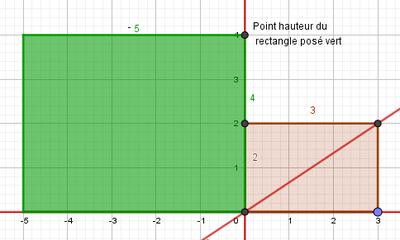
En vert, le rectangle posé représentant la fraction $\frac{-5}{4}$. Son sommet principal est de coordonnées $(-5 ;4)$.
Là aussi, pour faire le calcul on a deux méthodes similaires à celles de l’addition.
Autres exemples qui traitent du cas où la différence est négative.
Estimation d’un produit et de la racine carrée
Le but de cette partie est de montrer comment on pourrait utiliser les rectangles posés pour estimer rapidement avec une bonne précision le produit de deux nombres ainsi que la racine carrée d’un nombre positif.
Soient $B$ et $H$ deux nombres positifs. Pour le cas de nombres négatifs on prendra les valeurs absolues des nombres et on réglera l’histoire du signe à la fin, ou bien on appliquera la même méthode que l’on va décrire maintenant pour des bases ou des hauteurs négatives.
Géométriquement, on travaillera dans les autres quadrants du plan.
Soit $OACD$ un rectangle tel que $OA=B$ et $AC=H$. Soit $E$ un point appartenant à la demi-droite $[AC)$. La demi-droite $[OE)$ coupe $[DC)$ en $M$ comme sur la Figure 34 ci-dessous .
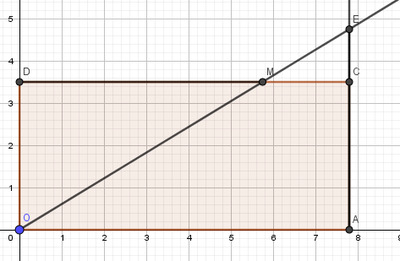
On trace la parallèle à $(AE)$ passant par $M$. Elle coupe $[OA]$ en $M’$, voir Figure 35 ci-dessous.
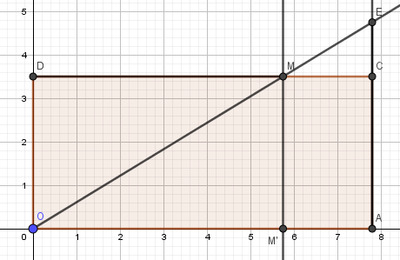
En appliquant le théorème de Thalès dans le triangle $OAE$ on a $\frac{OM’}{OA}=\frac{M’M}{AE}$ ou encore $\frac{DM}{B}=\frac{H}{AE}$ . L’égalité des produits en croix donne : $DM \times AE=B\times H$ (*).
En déplaçant le point $E$ sur la demi-droite $[AC)$, le point $M$ se déplace sur la demi-droite $[DC)$. Si le point $E$ va vers l’infini le point $M$ se rapprochera alors de $D$ et $DM$ tendra vers 0 et si $E$ tend vers $A$ alors le point $M$ tendra vers l’infini.
Selon la position de$E$ sur $[AC)$, différents cas se présentent donc :
- Quand $DM=1$, la relation (*) devient $AE=B×H$.
La position de $E$ donne alors la valeur du produit $B \times H$ (qui est aussi l’aire du rectangle $OACD$).
- Quand $AE=1$, la relation (*) devient $DM=B \times H$.
La position de $M$ donne alors la valeur du produit $B \times H$ (qui est aussi l’aire du rectangle $OACD$).
- Quand $DM=AE$, la relation (*) devient $DM^2 = AE^2 = B \times H$.
Ce qui signifie que $AE$ est la racine carrée du produit $B \times H$.
Si en plus $H$ est égal à $1$ on obtiendra alors une estimation de la racine carrée de $B$.
On vient de montrer comment on pourrait estimer géométriquement et rapidement le produit de deux nombres et la racine carrée d’un nombre rien qu’en déplaçant le point $E$.
Dans l’exemple illustré par les Figures 36 et 37 ci-dessous, on pourra lire l’estimation du produit $3,5 \times 7,8$ (dont la valeur exacte est $27,3$) et de sa racine carrée.
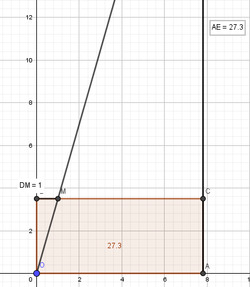
Figure 36 : Estimation au dixième près du produit $3,5 \times 7,8$. La valeur $27,3$ peut être lue sans difficulté sur une règle.
|
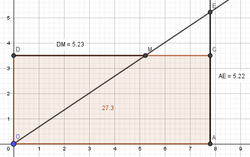
Figure 37 : Par lecture graphique, la racine carrée de $27,3$ est entre $5,22$ et $5,23$. Sur une règle on pourra lire sans difficulté la valeur arrondie au dixième.
La calculatrice donne la valeur approchée $5,224$. |
Remarques :
- Dans la démonstration on pouvait aussi utiliser le fait que les triangles $ODM$ et $EAO$ soient semblables et trouver l’égalité des rapports par proportionnalité des côtés.
- Si l’un ou les deux côtés du rectangle est(sont) trop petit(s) ou trop grand(s) on pourrait multiplier ou diviser le(s) côté(s) par des puissances de $10$ pour se ramener à une situation représentable géométriquement sur une fenêtre limitée (feuille ou écran).
Pour la racine carrée il faudra une multiplication ou une division de $B×H$ par une puissance de $100$.
- Selon la situation, pour améliorer la lecture de $AE$ dans l’estimation du produit, on pourrait aussi positionner $M$ de telle manière à ce que $DM$ soit égal à $2$ ; $4$ ; $5$ ou $10$.
On multipliera ensuite la valeur lue de $AE$ par l’une des valeurs choisies pour $DM$.
Si la valeur lue de $AE$ n’est pas précise, l’erreur d’estimation du produit augmente alors en multipliant par la valeur de $DM$.
- Avec la position $DM=2$, on obtient l’aire de n’importe quel triangle de base $B$ et de hauteur $H$.
Sur les Figures 38 et 39 on illustre ces situations pour l’exemple précédent :
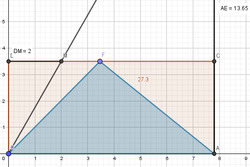
Figure 38 : Estimation d’un produit : Si le point $E$ est en dehors de la fenêtre de lecture, on pourrait jouer sur la position de $M$ pour faire rentrer $E$ dans la fenêtre de lecture. Ici avec $DM=2$, on obtient l’aire du triangle $OAF$ et l’aire de n’importe quel triangle de base $OA$ et de hauteur $H$.
|
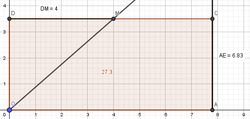
Figure 39 : Pour $DM=4$, la valeur lue de $AE$ est $6,83$. L’estimation du produit $B \times H$ s’obtient en multipliant cette valeur par $4$ mais dans ce cas l’erreur d’estimation augmente.
|
Multiplication de deux fractions
La multiplication de deux fractions peut être traduite géométriquement par l’étirement d’un rectangle posé dans deux directions orthogonales, l’une le long de l’axe des abscisses et l’autre le long de l’axe des ordonnées.
L’étirement dans une direction est une transformation géométrique qui consiste à dilater l’objet, d’un certain coefficient, le long de cette direction.
En se plaçant dans un repère orthonormé du plan, étirer une figure d’un coefficient $k>1$ le long de l’axe des abscisses revient à multiplier les abscisses de tous ses points par $k$ et de conserver leurs ordonnées.
De la même manière, étirer une figure d’un coefficient $k>1$ le long de l’axe des ordonnées revient à multiplier les ordonnées de tous ses points par $k$ et de conserver leurs abscisses.

Figure 40
Mona Lisa Image originale |

Figure 41
Étirement horizontal de deux fois |

Figure 42
Étirement vertical d’une fois et demie |
Étirer une figure d’un même coefficient $k>1$ le long des deux axes (abscisses et ordonnées) revient à faire un agrandissement de la figure de rapport $k$.
Ainsi la multiplication de deux fractions $a \over b$ et $c \over d$, où $b$ et $d$ sont non nuls, se traduit par l’étirement du rectangle posé de base $a$ et de hauteur $b$ dans le sens horizontal de coefficient $c$ et dans le sens vertical de coefficient $d$.
On pourrait aussi étirer le rectangle posé de base $c$ et de hauteur $d$ dans le sens horizontal de coefficient $a$ et dans le sens vertical de coefficient $b$.
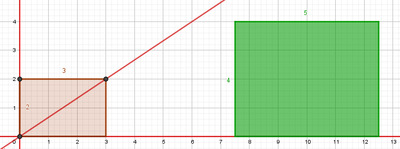
Sur la figure suivante on illustre le produit ${3 \over 2} \times {4 \over 5}$. Le rectangle posé de base $3$ et de hauteur $2$ est étiré horizontalement de $4$ fois puis étiré verticalement de $5$ fois, voir Figures 43 et 44.
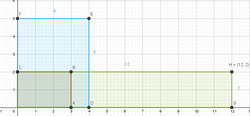
Figure 43 : Étirement horizontal de 4 fois
du rectangle posé marron. |
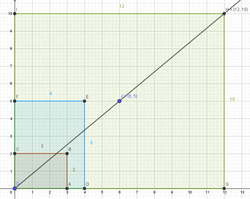
Figure 44 : Étirement Vertical de 5 fois
du rectangle posé vert. |
La diagonale principale du rectangle posé représentant le produit passe par le point de coordonnées entières $J(6 ;5)$. Le rectangle posé de base $6$ et de hauteur $5$ représente alors le résultat simplifié, voir Figure 45 ci-dessous.

Aller plus loin : étirement, lien avec théorème de Thalès et symétries
Pour mieux aborder l’étirement avec des notions du programme on fera dans ce paragraphe une belle approche en utilisant le théorème de Thalès et les symétries axiales ou les translations.
Soit $O$ un point du plan et $(d)$ une droite ne passant pas par $O$. Soient $M$ et $N$ deux points de $(d)$ à égale distance donnée de $O$. Soient $k$ un nombre réel supérieur à 1, $A$ et $B$ deux points appartenant respectivement à $[OM)$ et $[ON)$ tels que $OA=kOM$ et $OB=kON$ . La réciproque du théorème de Thalès nous assure que les droites $(MN)$ et $(AB)$ sont parallèles, voir la Figure 46 ci-dessous.
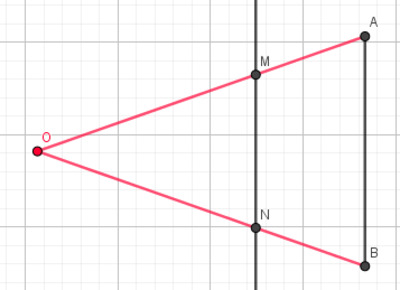
Soit $P$ le pied de la hauteur issue de $O$ dans le triangle $OMN$ et $H$ le pied de la hauteur issue de $O$ dans le triangle $OAB$, Figure 47. À nouveau le théorème de Thalès nous assure que $OH=k OP$.
Soit $E$ le symétrique de $O$ par rapport à $(AB)$. On a $EP=EH +HP$.
Puisque $EH=OH$ et $HP=OH-OP$ alors $EP=OH+(OH-OP)=2OH-OP$.
Ce qui donne $EP=(2k−1)OP$.
Ce qui signifie que si l’on déplace le point $O$ sur une distance dans une direction perpendiculaire à $(d)$ alors le point $E$ se déplacera sur une distance $(2k-1)$ fois plus grande et dans le sens opposé. Et si l’on déplace le point $O$ parallèlement à $(d)$ alors le point $E$ se déplacera parallèlement à $(d)$ de la même distance — propriété de la symétrie axiale car $(d)//(AB)$ — et dans le même sens que $O$, voir la Figure 47 ci-dessous.

Pour avoir l’étirement dans le même sens de déplacement de $O$ on prendra une symétrie axiale du point $E$ par rapport à $(d)$ — c’est-à-dire $(MN)$— soit $E’$ son image. La Figure 48 ci-dessous montre la trace du point $E’$ lorsque l’on déplace $O$.

Au passage, on remarque que $\frac{ED}{EA} = \frac{EP}{EH} = \frac{EP}{OH} = \frac{(2k-1)OP}{kOP} = \frac{2k-1}{k}$.
Donc $ED = E’D = \frac{2k-1}{k}OA = (2k-1)OM$ et $E’P = (2k−1)OP$. L’étirement est donc de coefficient $2k-1$ et de direction horizontale.
Le point $E$ est obtenu par symétrie axiale du point $O$ par rapport à $(AB)$. Le point $E’$ est obtenu par symétrie axiale du point $E$ par rapport à $(MN)$. Par conséquent, le point $E’$ est obtenu par la composition de deux symétries axiales d’axes respectifs parallèles $(AB)$ et $(MN)$. Ce qui signifie que $E’$ est l’image du point $O$ par la translation horizontale de vecteur $2 \times \overrightarrow{HP}$.
On sait qu’une translation est une isométrie (donc préserve les distances) alors que là on obtient un étirement. En fait, la position du point $H$ ainsi que celle de la droite $(AB)$ change en fonction de la position du point $O$. Cette translation « dynamique » n’est plus une translation au sens connu car son vecteur n’est pas fixe.
Sur la Figure 49 suivante on a caché quelques segments pour ne laisser apparaître que les segments nécessaires pour visualiser et comprendre l’étirement. Ceci nous donne la possibilité de fabriquer un instrument (pantographe) qui permet de faire les étirements, Figure 50.
Pour ce faire, les segments apparents sur la figure peuvent être remplacés par des baguettes plates percées aux points $O$, $M$, $N$, $A$,$B$, $E$, $D$, $F$ et $E’$ qui deviennent des points de pivotements. Les baguettes sont reliées entre elles aux points pivots par des vis sauf en $O$ et $E’$ qui doivent porter des stylos pour tracer. Des vis longues en $M$, $N$, $D$ et $F$ doivent coulisser sur une baguette qui représente la droite $(d)$.


Division de deux fractions
On sait que le quotient de deux fractions $\frac{a}{b} \div \frac{c}{d}$ est égal au produit $\frac{a}{b} \times \frac{d}{c}$. Pour donner une interprétation géométrique de la division on va utiliser l’égalité suivante : $\frac{a}{b} \div \frac{c}{d}=\frac{a \div c}{b \div d}$.
C’est une égalité qui n’est pas pratique en général puisqu’elle peut introduire dans les calculs des virgules et des nombres qui ne sont pas forcément décimaux, mais elle a un sens du point de vue géométrique puisqu’au lieu d’étirer les rectangles posés on va les contracter (les comprimer) dans les deux sens horizontal et vertical. À la fin on cherchera un rectangle posé similaire au rectangle posé contracté qui représente au mieux le quotient et dont le sommet principal est de coordonnées entières. Ceci peut se faire en agrandissant le rectangle contracté d’un coefficient égal à $c \times d$.
La base et la hauteur deviennent alors égales respectivement à $(a \div c) \times c \times d=a \times d$ et $(b \div d) \times c \times d=b\times c$ ce qui rejoint alors la formule donnant le produit $\frac{a}{b} \times \frac{d}{c}$.
Dans la Figure 51 suivante on donne l’exemple de la division $5 \over 4$÷$3 \over 2$=$5÷3\over 4÷2$. Le quotient de $5$ par $3$ n’est pas décimal et la valeur affichée de la longueur $FH$ de la base est approximative (ici à $10$ décimales près). La diagonale principale du rectangle posé OGHF passe par le point $J$ de coordonnées entières $(5 ; 6)$. Le quotient est alors égal à $5 \over 6$ et le rectangle posé $OKJL$ représentera alors mieux le quotient à la place de $OGHF$.
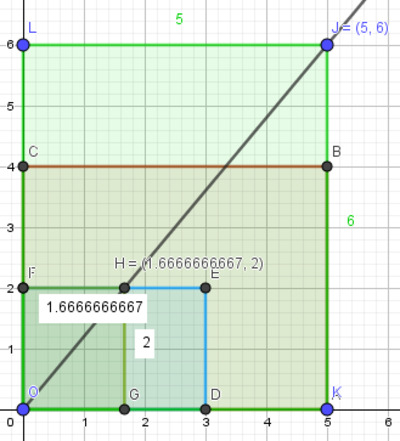
puis son agrandissement pour chercher un sommet principal $J$ de coordonnées entières.
Le « Fractiomètre »
Dans ce qui précède nous avons décrit comment, sur un simple quadrillage et une aiguille passant par le centre du repère, on pouvait faire géométriquement et visuellement des simplifications, des opérations sur les fractions, estimer la valeur décimale d’une fraction, faire un produit de deux nombres et chercher la racine carrée.
L’avantage de cette façon de faire est de permettre à l’élève de manipuler des entités géométriques, faire le lien entre une fraction et le rapport qui existe entre la longueur et la largeur d’un rectangle, découvrir la notion de pente d’une droite, sa caractérisation à travers d’une écriture fractionnaire, analyser l’exactitude d’une estimation, se passer d’une calculatrice, réviser ses tables de multiplication, faire implicitement des transformations géométriques (translation, symétries, homothéties, …).
Pour aller plus loin, on pourrait monter un projet avec les élèves pour fabriquer un instrument très simple qui fait ce travail. La fabrication de cet instrument impliquerait encore plus les élèves dans cette démarche et les pousserait à bien comprendre son fonctionnement et les bénéfices qu’ils pourraient en tirer.
La réalisation de cet instrument, que j’appellerais « Fractiomètre » ou « Fractiolabe », ne nécessite pas beaucoup de matériel ni de temps pour le réaliser. Il suffit d’un ancien calendrier en carton, un rouleau large de papier millimétré (pour éviter les collages approximatifs en format A4), une punaise et un fil de couture ou élastique fin (pour une meilleure précision de lecture) ou une longue règle en plastique transparent.
Le fil ou la règle joueront le rôle de la diagonale principale (droite pivotante passant par l’origine décrite plus haut dans les paragraphes précédents).
Pour finir, il faut fabriquer, avec du papier épais, plusieurs rectangles semblables de différentes tailles. Chaque famille de rectangles semblables doit avoir une couleur différente d’une autre famille comme ça les élèves pourront différencier rapidement une famille d’une autre.
La précision de lecture pour estimer des valeurs décimales dépend de la taille du « Fractiomètre ».
Une version virtuelle sur tablette pourrait donner de meilleures estimations. Les élèves pourront ainsi travailler sur une version numérique avec Scratch ou Python (pour ceux qui s’y intéressent déjà).
Je travaille actuellement avec mes élèves sur les deux versions. Voir par exemple le programme pour estimer une racine carrée.
Voici aussi un programme provisoire qui sert à ajouter deux fractions avec la méthode des rectangles posés.
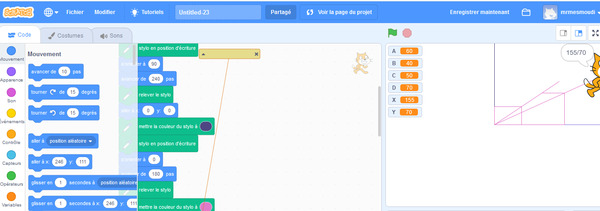
Conclusion
Dans cet article on traite le calcul fractionnaire d’une manière géométrique. On a fait le lien à plusieurs reprises entre la manière de faire le calcul ou les mesures et le théorème de Thalès et les transformations géométriques étudiées au collège.
Ce travail permet de concevoir un nouvel instrument manuel le « Fractiomètre » ou « Fractiolabe » pour aborder géométriquement le calcul fractionnaire et pour faire d’autres estimations.
La fabrication de ce nouvel instrument est en cours de réalisation avec un groupe d’élèves dans le cadre d’un projet. Ce dernier a évolué au fil des réflexions et du travail des élèves, et de nouvelles fonctionnalités du « Fractiomètre » ont été découvertes.
Ces fonctionnalités feront l’objet d’un article dans le prochain numéro des Chantiers.
La Régionale Île-de-France APMEP, 26 rue Duméril, 75013 PARIS