par Erwan Adam, Stéphan Petitjean
Atelier de la Journée de la Régionale
Lors de l’atelier de la matinée de la journée de la régionale d’Île-de-France de l’APMEP d’octobre 2020, nous avons présenté le site Rubricamaths. En voici le compte-rendu.
Rubricamaths est le site d’activités informatiques de l’IREM Paris-nord. Il comporte 400 activités environ, la plupart conçues sur le logiciel Geogebra. Les activités sont utilisables directement en ligne ou téléchargeables. Elles sont classées par thème dans des rubriques et des sous-rubriques.
Durant l’atelier du 17 octobre 2020, nous avons présenté succinctement le site et l’esprit qui sous-tend la conception et l’utilisation des activités. Nous développerons ici notre démarche au travers de quelques exemples que nous avons présentés lors de cet atelier.
Pour de plus amples détails, nous vous renvoyons à un article paru dans la rubrique multimédia du n°119 des repères-IREM en avril 2020, puis repris sur le site MathémaTICE en mai 2020.
La plupart des activités de Rubricamaths étant proposées en série, nous avons présenté sept types d’activités qui permettent d’avoir un aperçu des thèmes abordés et des pratiques pédagogiques qui leur sont associées :
- Géométrie dans l’espace : Visualiser des solides
- Nombres, variables et fonctions : Figures planes et figures discrètes
- Construction géométriques : Quadrilatères et parallélogrammes
- Les transformations du plan : Transformer à l’œil
- Les bases de la géométrie avec Géogebra
- Le compas dans l’œil : Géométrie mentale
- Construction géométriques : Construire de multiples manières
Un certain nombre de séries d’activités ont déjà fait l’objet d’articles détaillés. Nous ne nous étendrons donc pas sur celles-ci et nous contenterons d’une rapide description assortie de liens vers davantage d’informations. Pour les autres, nous nous appliquerons à décrire les activités, à détailler les objectifs pédagogiques et leur utilisation avec les élèves.
Géométrie dans l’espace : Visualiser des solides
Cette série d’activités propose des solides dont il faut déterminer le nombre de sommets, de faces et d’arêtes (et éventuellement la nature des faces). Le solide est manipulable par l’élève et les réponses peuvent être validées.
La série se trouve en suivant ce lien et le fichier utilisé pour la démonstration est le tétrakaidécaèdre. Un article détaillant le fonctionnement de ces activités est disponible en suivant ce lien : Visualiser dans l’espace pour dénombrer.
Nombres, variables et fonctions : Figures planes et figures discrètes
Dans cette série d’activités, une figure plane dépendant d’une variable est proposée. Cette variable prend des valeurs discrètes et peut varier en actionnant un curseur.
L’objectif est de déterminer l’expression du périmètre et de l’aire de cette figure en fonction de la variable. Pour aider et favoriser la conjecture, l’élève peut tester des valeurs entières dans un tableur dans lequel les réponses sont validées. Les expressions littérales peuvent elles aussi être validées quelle que soit leur forme. Cela en fait un point fort de cette série car elles permettent à l’enseignant de revenir sur les règles de calcul littéral pour justifier les égalités d’expressions.
La série se trouve en suivant ce lien et le fichier utilisé pour la démonstration est le carré tronqué (1) .
Un article détaillant le fonctionnement de ces activités est disponible en suivant ce lien : Figures et variables discrètes.
Construction géométriques : Quadrilatères et parallélogrammes
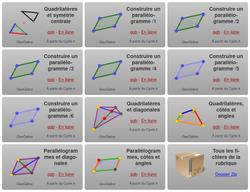
Cette série d’activités est différente des autres car il y a trois types de fichiers avec des fonctionnements différents. Chacun de ces types de fichiers permet de travailler diverses compétences sur les quadrilatères et le parallélogramme :
- L’activité « Quadrilatère et symétrie centrale » permet de découvrir les propriétés du parallélogramme en le liant à une situation de symétrie centrale.
- Les activités « Construire un parallélogramme » ont vocation à mettre en œuvre les propriétés du parallélogramme dans l’objectif de le construire. Ici, les outils à disposition sont réduits afin de forcer la méthode de construction. Il est possible pour l’élève de valider sa construction.
- Les activités suivantes permettent de travailler sur les propriétés caractéristiques des quadrilatères et du parallélogramme. Ce sont ces activités que nous allons détailler.
Nous prendrons comme exemple l’activité « Quadrilatères et diagonales » accessible en suivant ce lien.
Dans cette activité, nous disposons de deux segments pour lesquels nous pouvons agir sur les longueurs (curseurs), l’orientation (points jaunes) et la position sur l’écran (points rouges). Nous nous apercevons rapidement que ces deux segments sont les diagonales d’un quadrilatère et qu’il nous faut les disposer de manière à obtenir des quadrilatères particuliers : parallélogramme, rectangle, trapèze…
Pour aider à disposer les segments dans les positions adéquates, les points rouges placés au milieu des diagonales sont aimantés à l’autre diagonale. L’angle droit entre deux diagonales est lui aussi aimanté de manière à être obtenu facilement.

Ainsi, l’élève a tout loisir d’expérimenter, d’essayer jusqu’à obtenir une figure qui le satisfasse. Lorsqu’il pense avoir trouvé l’une des figures demandées, par exemple le rectangle, il lui est demandé d’écrire une propriété caractéristique qui correspond à la situation : un quadrilatère ayant ses diagonales qui ont le même milieu et qui sont de même longueur est un rectangle.
C’est ce travail de rédaction qui nous semble important car il permet de vérifier si l’élève a compris. En effet, les figures en elles-mêmes sont assez faciles à trouver par essais successifs. En revanche, il ne sera pas rare de voir les élèves écrire :
- « un quadrilatère ayant quatre angles droits est un rectangle » (1)
- « un quadrilatère ayant ses diagonales de même longueur est un rectangle » (2)
- « le rectangle a ses diagonales de même longueur et qui se coupent en leur milieu » (3)
Dans chacune des affirmations précédentes, il est possible pour l’enseignant d’infirmer la proposition erronée ou incomplète de l’élève en précisant de nouveau qu’elles sont les données de départ et en manipulant sa figure. Ainsi :
- L’affirmation (1) est contredite par ce qui est mis à disposition de l’élève, à savoir les diagonales. La propriété produite par l’élève est donc correcte mais hors-sujet. Si lui faire remarquer ne suffit pas, la manipulation devant lui des différents degrés de liberté de la figure peut permettre de le convaincre car ce qui reste fixe est alors plus visible.
- L’affirmation (2) peut facilement être infirmée en disposant les diagonales comme dans la propriété proposée, c’est-à-dire sans que les diagonales se coupent en leur milieu. Le quadrilatère obtenu n’étant pas un rectangle, nous faisons prendre conscience à l’élève que sa propriété est incomplète. Nous pouvons alors l’aider à la formuler correctement.
- L’affirmation (3) est plus difficile à contredire puisque l’élève a écrit une propriété, juste au demeurant (un rectangle a bien ses diagonales de même longueur et qui se coupent en leur milieu), et non une propriété caractéristique, c’est-à-dire une propriété avec des conditions nécessaires et suffisantes permettant d’obtenir la figure demandée (un quadrilatère ayant ses diagonales de même longueur et qui se coupent en leur milieu est nécessairement un rectangle).
Ici, nous rentrons au cœur même de l’activité et les élèves vont avoir des degrés de compréhension très hétérogènes de cette notion.
Certains d’entre eux ne parviendront d’ailleurs pas à s’en faire une idée claire après avoir effectué cette activité tant cette notion demande un degré d’abstraction important. Il faut donc faire attention à ne pas laisser l’élève passer trop de temps sur la même situation et à ne pas insister de manière trop poussée sur les formulations car cela pourrait s’avérer contre-productif.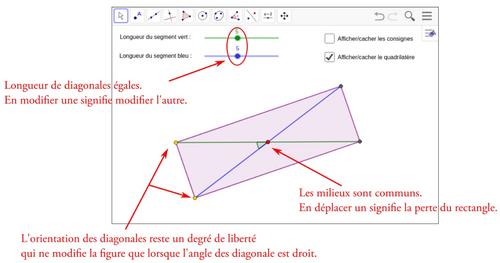
Trois autres fichiers permettant de travailler sur les propriétés caractéristiques sont disponibles dans cette série :
- Parallélogrammes et diagonales
- Quadrilatères, côtés et angles
- Parallélogrammes, côtés et angles
Ces fichiers permettent de varier les situations. Il n’est sans doute pas nécessaire de tous les proposer à chaque élève, nous pouvons tout à fait nous servir de ces fichiers en classe entière comme base d’un débat.
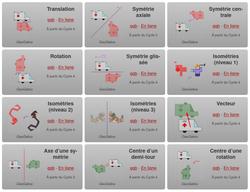
Les transformations du plan : Transformer à l’œil
Dans les activités de cette série, il faut déplacer la figure bleue dans la bonne position par rapport à une transformation donnée. L’élève valide sa réponse et un score apparait dans un tableur. Une situation similaire lui est alors proposée. L’objectif principal de ces fichiers est de permettre à l’élève de s’entraîner et de se forger une bonne image mentale des différentes transformations du plan.
La manipulation aisée et la validation immédiate permettent aux élèves de réaliser de nombreuses constructions en un temps court.
La série se trouve en suivant ce lien. Plusieurs de ces fichiers ont été utilisés. Une description plus détaillée de cette série est accessible dans l’un des paragraphes de l’article accessible en suivant ce lien.
Les bases de la géométrie avec Géogebra
Cette série d’activités informatiques est à mener conjointement avec des activités sur support papier.
En effet, ces deux supports sont complémentaires. Les activités informatiques sont accessibles à cette adresse tandis que les activités papiers, tirées de la brochure Papiers Crayons se trouvent en suivant ce lien.
Le principe général est de reproduire la figure donnée à partir des points ou lignes qui sont fournis au départ. Cette série suit une progression bien déterminée avec certains passages obligés qui peuvent présenter des difficultés pour les élèves.
Vous trouverez une description détaillée des principes et des modalités d’utilisation de ces activités, qu’elles soient sur papier ou sur Geogebra, dans la préface de la brochure Papiers Crayons.
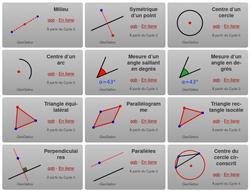
Le compas dans l’œil : Géométrie mentale
Cette série d’activités vise à entraîner l’œil à voir des lignes non tracées. Elles se présentent toutes de la même façon : l’élève doit cliquer au jugé pour placer un point comme une intersection de droites qui ne sont pas tracées entièrement, un centre de cercle ou d’arc de cercle, l’image d’un point dans une symétrie, etc.
L’objectif de cet entraînement est double : d’abord, il facilite l’apprentissage de toutes les constructions géométriques — l’élève qui a déjà dans l’œil la position de la perpendiculaire n’a aucun mal à placer son équerre pour la construire — ensuite il prépare à l’abstraction en rendant les élèves capables de parler de lignes géométriques qui ne sont pas visibles. Il développe aussi par ces activités des compétences utiles en dessin, en particulier une bonne intuition des proportions.
Ces activités sont conçues pour être faites rapidement de façon à multiplier les essais. Elles peuvent par exemple être proposées en début d’heure en salle informatique, pendant 10 minutes — au-delà, il faut ménager une pause pour les yeux. On peut aussi demander aux élèves qui le peuvent de s’entraîner à la maison. Les progrès des élèves, même en quelques séances de 10 minutes, sont rapides et visibles pour eux (par le score).
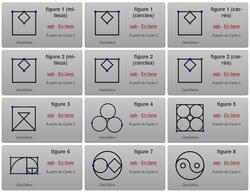
Constructions géométriques : Construire de multiples manières
Cette série est composée d’activités qui sont autant de problèmes de construction s’adressant plutôt à des élèves de 6e.
Le principe est de reproduire la figure à partir des points donnés en utilisant les outils à disposition. Les activités sont de difficulté progressive :
- Les six premiers problèmes font appel à la même situation géométrique mais les outils à disposition varient ainsi que les points donnés au départ.
- Le sept problèmes suivant sont des situations uniques.
Les constructions peuvent être validées par les élèves de deux manières, soit en cliquant sur le bouton « valider », soit en déplaçant les points libres tout en vérifiant que la figure reste la
même.
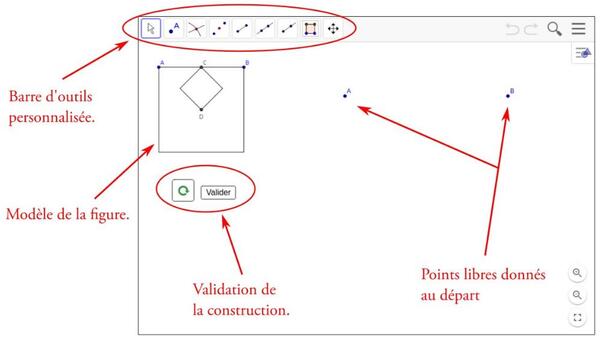
Les fichiers utilisés pour la démonstration sont les 3 premiers, c’est-à dire : figure 1 (milieux), figure 1 (cercles) et figure 1 (carrés).
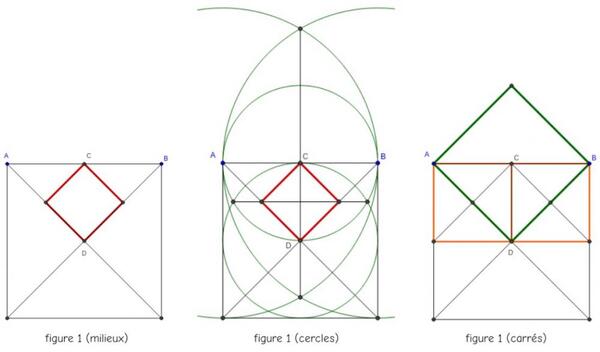
L’intérêt majeur de cette série d’activités est la limitation des outils mis à disposition de l’élève. Cela permet en effet de favoriser une certaine démarche de construction par rapport à d’autres. Ainsi dans les trois fichiers pris en exemple, le même problème ne peut pas être résolu avec la même méthode :
- Dans le premier « figure 1(milieux) », la présence de l’outil « milieu » rend la construction assez aisée à partir du moment où l’on pense à tracer les diagonales.
- Dans le deuxième « figure 1(cercles) », l’absence de l’outil « milieu » rend obligatoire l’utilisation des cercles pour obtenir les milieux par le tracé de médiatrice.
- Dans le troisième « figure 1(carrés) », on donne à l’élève la macro « carré » seulement, un outil spécifique au logiciel qui n’a pas d’équivalent sur support papier. Cela permet une résolution plus atypique de ce problème.
Avec les trois figures suivantes, nous complexifions encore le même problème en changeant les points donnés au départ. Par la suite, les problèmes sont uniques et graduels. Ceux de la fin de la série représentent de vrais défis de construction. Cela permet de gérer l’hétérogénéité des élèves, chacun ayant son propre rythme de progression.
Conclusion
Bien d’autres séries de fichiers sont disponibles sur Rubricamaths que ce soit dans le domaine de la géométrie dans l’espace, dans le domaine des variables ou de la géométrie à l’œil.
Nous espérons vous avoir convaincu de visiter notre site et de proposer certaines de nos activités à vos élèves. En tous cas, nous espérons que la lecture de ces quelques lignes vous aura donné l’envie d’essayer.
La Régionale Île-de-France APMEP, 26 rue Duméril, 75013 PARIS