Solution de l’avis de recherche n°8

Énoncé de l’avis de recherche n°8 (rappel) :
Il s’agit de contempler ces 65 exemplaires du même ennéagone "crevette" ci-dessous, de déterminer ses côtés et ses angles et d’utiliser ces résultats pour trouver les pavages possibles du plan avec cette crevette… s’il en existe !

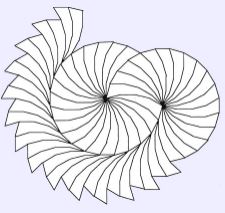
Envoyer vos réponses à esartinuloc chez gmail.com

Une seule réponse complète à ce dernier avis de recherche : celle du fidèle Couzineau qui a calculé les dimensions de la crevette et présenté un certain nombre de pavages possibles.

I. Dimensions de l’ennéagone

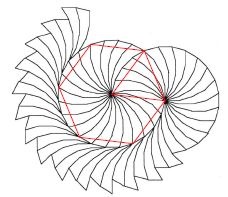
On considère vraies les informations données par la figure. L’ennéagone est construit à partir d’un polygone régulier à 24 côtés. L’imbrication au centre donne l’égalité de tous les côtés de l’ennéagone. On peut faire ressortir cette propriété à l’aide d’une partie d’hexagone régulier inscrit.

Un polygone régulier à $n$ côtés,de mesure $c$, est inscrit dans un cercle de rayon $R$. Par des calculs classiques (que je ne détaille donc pas), on a :

$$ \tan \left( \dfrac{1}{2} \times \dfrac{360^\circ}{n} \right) = \dfrac{c}{2R} $$

Pour le calcul des angles, j’utilise la propriété suivante bien connue : la somme des angles dans un polygone strictement convexe à $n$ côtés vaut $ 180^\circ \times (n - 2) $.

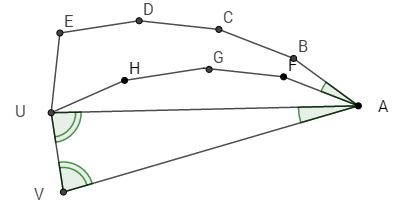
Dans le triangle $AUV$, l’angle en $A$ vaut $\alpha= \dfrac{360^\circ}{24} = 15^\circ$ et l’angle en $V$ vaut $\beta = \dfrac{1}{2} (180^\circ - \alpha) = 82,5^\circ$.

Dans l’ennéagone ABCDEUHGF, l’angle en $A$ vaut $\alpha$ et les angles intérieurs en $B$, $C$ et $D$ et extérieurs en $F$, $G$ et $H$ valent $2\beta$ par construction.

Dans le pentagone $AFGHU$, les angles en $A$ et $U$ valent donc $\theta = \dfrac{1}{2} (180^\circ \times 3 - 3\times 2\beta) = 22,5^\circ$.

Dans le triangle $AUE$, l’angle en $U$ vaut $\beta$ donc, dans l’ennéagone, l’angle en $U$ vaut $\theta = \beta - \delta = 60^\circ$.

Enfin, dans l’ennéagone, l’angle en $E$ vaut $ \gamma = 180^\circ \times 7 - \alpha - 3 \times 2\beta - 3(360^\circ - 2\beta) - \theta = 105^\circ$.

II. Pavages du plan

Avec les notations de la figure précédente, la motif présenté ci-contre possède des angles plat (sur les bords). En effet, les angles en $A$, $E$ et $U$ forment un angle de $\alpha + \theta + \gamma = 15^\circ+60^\circ+105^\circ = 180^\circ$. Les ennéagones étant identiques, les deux côtés de la figure sont parallèles et le pavage du plan est possible.

Avec le motif précédent, on peut construire certains des 17 pavages périodiques du plan (exemples ci-dessous). Comme je ne maîtrise pas suffisamment les pavages périodiques, je ne les identifierais pas.

On peut aussi trouver des pavages non périodiques. Par exemple, en s’inspirant de l’image initiale, on peut paver le plan par couches concentriques dont les bords forment, par construction, des 24-gones réguliers (ce pavage n’est pas périodique car aucune translation n’est possible).

Et avec une tortue

Bien que n’ayant pas envoyé une solution au sens habituel du terme, l’autre fidèle, Salvatore Tummarello, a demandé à la célèbre tortue de reproduire la figure de l’énoncé prouvant ainsi qu’il avait tout compris (les angles sont les bons) et qu’il avait bien expliqué à la tortue ce qu’elle devait faire car si la tortue logo a acquis de la vélocité en revanche elle ne brille toujours pas par l’esprit.

Si vous voulez voir la tortue au travail il vous suffira de recopier les deux procédures ci-contre (l’une pour tracer la crevette et l’autre pour la figure) sur Géotortue que vous pouvez obtenir sur le site geotortue.free.fr

Et cela m’a inspiré une démonstration qui me semble plus "naturelle" des propriétés de la crevette…

Imaginez 2 tortues partant de $A$, une bleue suivant le trajet $ABCDE$ et une rouge suivant le trajet $AIHGF$.

Les renseignements obtenus sur la figure permettent de savoir facilement que les deux trajets sont les mêmes (même longueur des segments et mêmes angles de rotation dans les tournants donc $\beta = \gamma$) et qu’ils sont simplement déduit l’un de l’autre par une rotation de centre $A$ et d’angle $\alpha = 15^\circ$ comme montré par Jean Couzineau.

Mais il faut se concentrer davantage pour comprendre que $\alpha=\beta$ : l’alignement des points $O,A,I$, $(AI)$ bissectrice de l’angle $\widehat{BAC}$ (qui vaut $2\beta$) permettent de conclure à l’égalité des angles ci-dessus.

Cette égalité des angles permet de voir la crevette comme une succession de losanges $ABCI$, $ICDH$, $HDEG$ et d’un demi losange $GEF$ d’angle aigu $\alpha$, $2\alpha$, $3\alpha$, $4\alpha$ qui permettent de donner facilement la valeur de tous les angles de l’ennéagone-crevette.

Et de se demander si l’on peut construire des crevettes vérifiant ces contraintes (côtés égaux et angle de départ $\alpha$ et angle de "virage" égaux à $\alpha$) à 3 côtés (oui : c’est un triangle équilatéral), 5, 7, 11,13… côtés et quelles sont leurs propriétés ?

Et un autre pavage

J’ai retrouvé sur internet le livre qui a vraisemblablement servi à tonton Lulu pour extraire ce début de pavage. Il est en anglais (of course) intitulé Tilings and Patterns de Branko Grünbaum et G.C. Shephard dont vous pouvez feuilleter quelques pages.

Avis de recherche n°9 ?

pas d’énoncé puisque celui-ci était le dernier et qu’aucun repreneur ne s’est présenté… pour l’instant… mais il sera toujours temps de reprendre ces Avis de Recherche sous la même forme ou une autre si un (ou plusieurs) de nos adhérents veu(len)t bien l’animer.