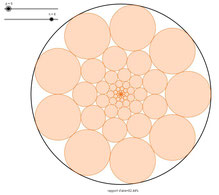
par Alain Bougeard
Solution de l’avis de recherche n°4
L’avis de Recherche n° 4 a donné lieu à une intense activité à laquelle ont participé par échange de méls, outre les auteurs de cet avis, Jean Couzineau le premier à réagir, les animateurs de l’IREM Salvatore Tummarello et Stéphan Petitjean ainsi qu’une longue discussion sur le forum de GeoGebra, aboutissant à la création de la solution GeoGebresque de Noël Lambert.
Le problème pour moi est de faire le compte rendu de tout cela dans une longueur raisonnable, sans oublier les apports de chacun et en traduisant tout cela en html. Je sais d’avance que c’est raté mais je vais essayer de faire de mon mieux...
On peut cliquer sur toutes les figures pour les agrandir ou les ouvrir dans GeoGebra.
Pour la clarté de ce qui va suivre on appelle $p$ le nombre de cercles dans une ronde et $n$ le nombre de rondes.
Constructions à la règle et au compas
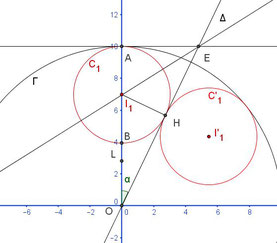
La construction à la règle et au compas de la première ronde de $p$ cercles est facile… à condition de savoir construire un angle de $ \alpha = {\displaystyle \pi \over \displaystyle 2p}$ c’est à dire un polygone régulier à $p$ cotés. Et pour cela il faut aller voir du côté de Gauss-Wantzel pour savoir ceux qui sont constructibles… Heureusement que les traceurs modernes se sont affranchis de cette contrainte.
La droite $\Delta$ passant par $O$ étant tracée ainsi que la tangente $T$ au cercle $\Gamma$ en $A$, il suffit de tracer la bissectrice passant par le point d’intersection $E$ et de prendre son intersection avec $(OA)$ pour obtenir le centre $I_1$ du premier cercle de la ronde. Les $p$ autres s’obtiennent par rotations successives de centre $O$ et d’angle $2\alpha$ à partir du premier cercle de la ronde.
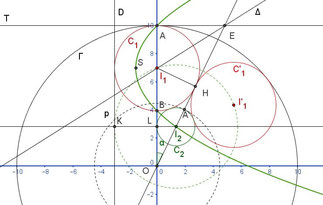
Pour construire un cercle de la 2e ronde Jean Couzineau et moi avons opté pour la méthode consistant à construire le cercle $C_2$, tangent à $C_1$ et $C’_1$ d’abord comme le cercle tangent à $C_1$ et l’axe des $y$.
C’est une méthode "classique" (c’est à dire que je la connais…) que de construire les centres des cercles tangents à un cercle $C_1$ et une droite (l’axe des $y$) en remplaçant cette construction par celle des centres des cercles tangents à la droite $D$ (translatée de l’axe des $y$ par le vecteur $(-r,o)$ où $r$ est le rayon du cercle $C_1$) et passant par le point $I_1$, cet ensemble de points étant la parabole $\Pi$ de Foyer $I_1$ et de directrice $D$.
Il ne reste plus qu’à construire l’intersection de la parabole $\Pi$ avec la droite $\Delta$. Là encore il s’agit d’un problème "classique" (même définition...). Je ne veux pas alourdir la démonstration mais ceux qui sont intéressés peuvent l’obtenir en cliquant ici.
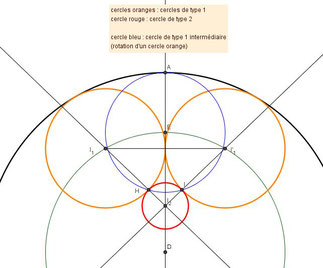
D’autant plus que Stephan Petitjean nous a envoyé une construction nettement plus efficace pour les cercles de la 2e ronde.
Mais sans justifications...
C’est un sangaku…
…regardez et comprenez !
Calculs
Tous les participants ont d’une façon ou d’une autre été obligés de se livrer à ces calculs et de trouver les mêmes résultats sous une forme plus ou moins appétissante. J’ai choisi la solution de Salvatore Tummarello qui m’a paru la plus efficace de toute (y compris la mienne...).
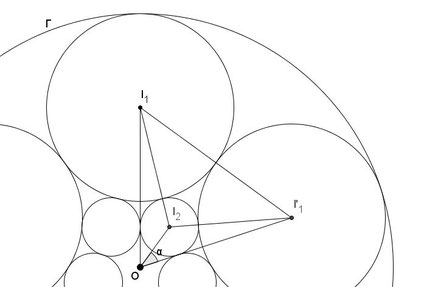
Sans perte de généralité, on suppose que le grand cercle $\Gamma$, de centre $O$, a pour rayon 1.
Sur la figure, on voit que $\alpha = {\displaystyle \pi \over \displaystyle p}$ où $p \geq 3$ désigne le nombre de cercles de chaque ronde
On note $r_n$ les rayons des cercles de la $n$-ième ronde, et $l_n$ la distance commune entre leurs centres et l’origine $O$.
Pour la première ronde, avec $OI_1=1−r_1$ et $2r_1 = I_1I’_1 = 2OI_1\sin(\alpha)$,
on trouve $r_1=(1−r_1)\sin(\alpha)$, puis $r_1 = {\displaystyle \sin(\alpha) \over \displaystyle 1 + \sin(\alpha)}$.
De plus, $l_1 = 1−r_1 = {\displaystyle 1 \over \displaystyle 1+\sin(\alpha)}$.
Pour les rondes suivantes, on voit facilement que $r_n = l_n \sin(\alpha)$, et l’on s’intéresse au rapport $k_n = {\displaystyle l_{n+1} \over \displaystyle l_n} = {\displaystyle r_{n+1} \over \displaystyle r_n}$, que nous allons calculer.
La formule d’Al-Kashi appliquée au triangle $OI_2I1$ s’écrit : $\left(r_n+r_{n+1}\right)^2 = l_{n+1}^2+l_n^2-2l_nl_{n+1}\cos(\alpha)$
En divisant cette relation par $l_n^2$, on obtient : $\left(\dfrac{r_n+k_nr_n}{l_n}\right)^2 = k_n^2+1-2k_n\cos(\alpha)$
puis $(k_n+1)^2\sin^2(\alpha) = k_n^2+1-2k_n\cos(\alpha)$
d’où l’équation du second degré en $k=k_n $ (sans surprise, $k_n$ ne dépend pas de $n$) :
$k^2\cos^2(\alpha)-2k\left(\cos(\alpha)+\sin^2(\alpha)\right)+\cos^2(\alpha)=0$
Le discriminant réduit de ce trinôme vaut :
et on obtient pour solutions : $k_± = {\displaystyle \cos(\alpha) + \sin^2(\alpha) ± \sin(\alpha) \sqrt{2\cos(\alpha) + 1} \over \displaystyle \cos^2(\alpha)}$
Les relations coefficients-racines montrent facilement que $k_+ \times k_− = 1$ et $k_+ + k_− \gt 0$.
La valeur de $k$ cherchée (plus petite que 1) est donc :
$k_n$ étant constant, les suites $(r_n)$ et $(l_n)$ sont géométriques, d’où leur expression en fonction de $n$ et $\alpha$ :
$l_n = l_0k^n = {\displaystyle k^n \over \displaystyle 1 + \sin(\alpha)}$
Remarque : Les calculs ci-dessus prouvent que $k \lt 1$ et par conséquent que les cercles de la deuxième ronde sont strictement plus petits que ceux de de la première… sauf si la seconde ronde se réduit à un cercle tangent à tous les autres ! Regardez ici.
Avec GeoGebra…
Deux réalisations :
La première de Stéphan Petitjean, classique, variant avec les curseurs $p$ et $n,$ par la création de listes.
Pour voir le fonctionnement et surtout avoir les détails de la programmation cliquez sur l’image ci-contre.
La seconde, plus sophistiquée, paraît incompréhensible si l’on examine le "programme". Il faut avoir la curiosité d’aller regarder dans les propriétés du curseur de $p$ (non, dans $n$ il n’y a rien...) pour découvrir les 3 lignes de script qui révèlent les secrets du mystère.
Normal, c’est l’œuvre de Noël Lambert himself, le traducteur français de Geogebra et le créateur des manuels d’aide, qui l’a faite après discussion sur le forum de GeoGebra.
Merci Noël !
Allez vite voir cela en cliquant sur la rose de Noël ci-contre.
Avec GéoTortue…
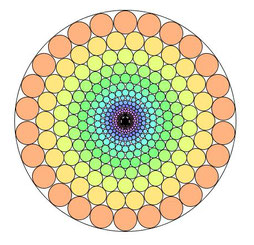
Avec GéoTortue (avec un accent aigu car c’est un logiciel français…) les couleurs ont été soignées mais le programme de Salvatore Tummarello, créateur entre autre de GéoTortue, l’est tout autant.
Il a même utilisé une procédure "cachée" : _cercle…
Je suis toujours étonné de voir comment on peut expliquer à une petite tortue de faire autant de choses en si peu de mots…
Par contre si vous voulez voir cela il vous faudra le mériter :
- d’abord télécharger la version 4 (qui est encore Béta mais plus pour longtemps)
- Ensuite télécharger le fichier RondesTortues.trt, le dézipper et le mettre dans un endroit sûr.
- Puis après ouverture de GéoTortue vous pourrez alors aller chercher le fichier RondesTortues.trt dans l’endroit sûr et l’ouvrir (attention ce fichier n’est pas auto-exécutable donc il faut procéder comme indiqué ci-dessus).
- Et pour finir la récompense : en tapant mg ; mg zoom 200 ; ronde 26 15 vous verrez la tortue faire ses rondes folles.
Et vous pourrez recommencer avec 36 15 si cela vous chante ou tout autre choix de $n$ et $p$, à condition de faire un vg (vide graphique) avant chaque nouvelle ronde…
Et la (les) limite(s)
Tous ceux qui ont abordé cette question (soit expérimentalement avec GeoGebra ou GéoTortue soit par le calcul comme Couzineau ou Tummarello) on bien senti la difficulté de chercher une limite d’une fonction à deux variables $A(n,p)$. En effet :
Le pourcentage de la somme des aires des cercles sur l’aire du grand cercle est :
$P_{n,p} = {\displaystyle 1 \over \displaystyle \pi} \displaystyle \sum_{i=1}^{n} i \pi r^2_i = \displaystyle \sum_{i=1}^{n} p\left({\sin(\alpha) \over 1 + \sin(\alpha)}\right)^2 k^{2n} = p{\displaystyle \sin^2(\alpha) \over \displaystyle \left(1 + \sin(\alpha)\right)^2}{\displaystyle 1 - k^{2n+2} \over \displaystyle 1 - k^2}$
Si l’on considère que les variables $n$ et $p$ sont indépendantes on peut commencer par examiner deux cas :
- $n$ fixé, on fait tendre $p$ vers l’infini (avec $sin\alpha= {\displaystyle \pi \over \displaystyle n}$).
On voit facilement que $P_{n,p}$ tend vers 0
- $p$ fixé, on fait tendre $n$ vers l’infini.
D’après l’expression de $k$ il est facile de démontrer que $k \approx 1 - {\displaystyle \pi \over \displaystyle p} \sqrt{3}$
et donc : $1 - k^2 \approx 1 - 1 - {\displaystyle 3 \pi^2 \over \displaystyle p^2} {\displaystyle 2\pi \over \displaystyle p} \sqrt{3}$
D’où : $P_{n,p} \approx {\displaystyle p \pi^2 \over \displaystyle p}\times{\displaystyle p \over \displaystyle 2\pi\sqrt{3}} = {\displaystyle \pi \over \displaystyle 2\sqrt{3}} \approx 0,9069$ noté $L$.
Ce que l’on peut vérifier expérimentalement sur toutes les représentations graphiques.
Mais bien sûr cela ne prouve rien quant à la définition d’une limite… (une vraie).
Jean Couzineau a exploré le cas où $m=n$ mais seul Salvatore s’est aventuré plus loin de façon très expérimentale que je vous livre telle quelle :
En revanche, on peut faire croître $n$ et $m$ conjointement. Après quelques bidouilles avec maxima, j’ai remarqué que si $n$ est négligeable devant $m$, la limite est nulle, tandis qu’inversement si $m$ est négligeable devant $n$, la limite est $L$ (en même temps, quand je dis négligeable, je n’ai testé pas avec $m=n \log(n)$… ).
Entre ces deux extrêmes, il est intéressant de remarquer que si $n$ et $m$ dépendent linéairement l’une de l’autre, disons $n=am$, alors un facteur de correction surgit : la limite vaut dans ce cas ${\displaystyle \pi \over \displaystyle 2\sqrt{3}} \times {\displaystyle \left(1 - e^{\displaystyle -2\pi\alpha\sqrt{3}}\right)}$ (je ne l’ai pas fait à la main, mais ça doit se faire avec des développements limités d’ordre 1). Ma conclusion sur la majoration reste donc valable ! :D (mais la démonstration ne tient pas dans la marge de ce courriel).
Évidemment cela ne résout pas le cas où le point $M(n,p)$ irait rejoindre l’infini en suivant une spirale d’Archimède ou de Bernouilli ou autre méthode bizarre…
Ce qui prouve que la recherche reste ouverte. Si cela vous tente…
Et en prime…
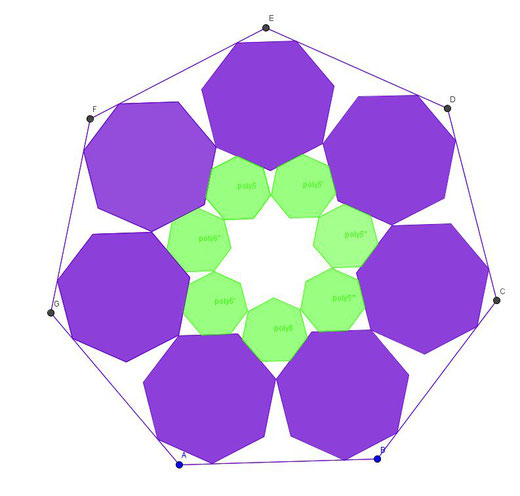
Et pourquoi se contenter de cercles ?
On peut se poser la question pour des triangles, des quadrilatères, etc. à condition de définir la notion de tangence pour des polygones.
Ici par exemple avec des heptagones réguliers…
Avis de Recherche n°5
Énoncé de l’avis de recherche n°5 :
Soit un trapèze, dont les longueurs des bases sont $a$ et $b$, coupé en deux parties de même aire par un segment de longueur $c$ parallèle aux bases.
Peut-on avoir $a$, $b$ et $c$ entiers ?
Et puis peut-on le couper de la même façon par deux segments de longueur $c$ et $d$ avec $a$, $b$, $c$ et $d$ entiers ?
Et par $n$ segments… ?
La Régionale Île-de-France APMEP, 26 rue Duméril, 75013 PARIS